Integrale von Produkten zweier Sinusschwingungen ungleicher Frequenzen sind immer Null. Wenn die Frequenzen gleich sind, ist das Integral π. Das wollen wir ausnahmsweise nicht beweisen, sondern grafisch plausibilisieren.
Bewege die beiden Schieberegler, um die jeweilige (ganzzahlige) Frequenz für die orangefarbene bzw. die blaue Sinus-Schwingung einzustellen. Die weiße Fläche stellt das Integral des Produkts (Multiplikation) der beiden Sinusschwingungen zwischen 0 und 2π dar. Überraschend ist, dass dieses Integral immer den Wert 0 hat, außer, die beiden Frequenzen sind gleich, dann hat dieses Integral den Wert π. Dies lässt sich grafisch plausibilisieren, wenn man die Verteilung von weißen Flächenanteilen ober- und unterhalb der x-Achse anschaut. Diese Tatsache ist gleichermaßen faszinierend wie nützlich als Grundlage für die Fourier-Analyse, d. h. die Zerlegung von komplexen Schwingungen in einzelne Sinus-Schwingungen mit ganzzahliger Frequenz („harmonische Oberschwingungen“).
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Fourier-Reihe der Rechteckfunktion? Hart? Auf jeden Fall. Hier wird's veranschaulicht.
Fourier-Transformation zum Leben erweckt. Jetzt wird's endlich klar...
Sinus und Kosinus im Gewand der komplexen Exponentialfunktion. Exotisch.
Sinusschwingungen verschiedener Frequenz multipliziert verhalten sich komisch.
Ein Kreis, der sich auf einem Kreis dreht. Abgedreht. Muss man auf sich wirken lassen.
Sinus und Kosinus: Wir stauchen, schieben und strecken sie hart. Und Trocken.
Come on crazy party people make some noise! Lautsprecher an und los geht's!
Kreise sitzen auf Kreisen, die auf Kreisen sitzen, die auf Kreisen sitzen, die auf...
Zeichne eine beliebige Figur und lasse sie nachzeichnen von Kreisen, die auf Kreisen sitzen.
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
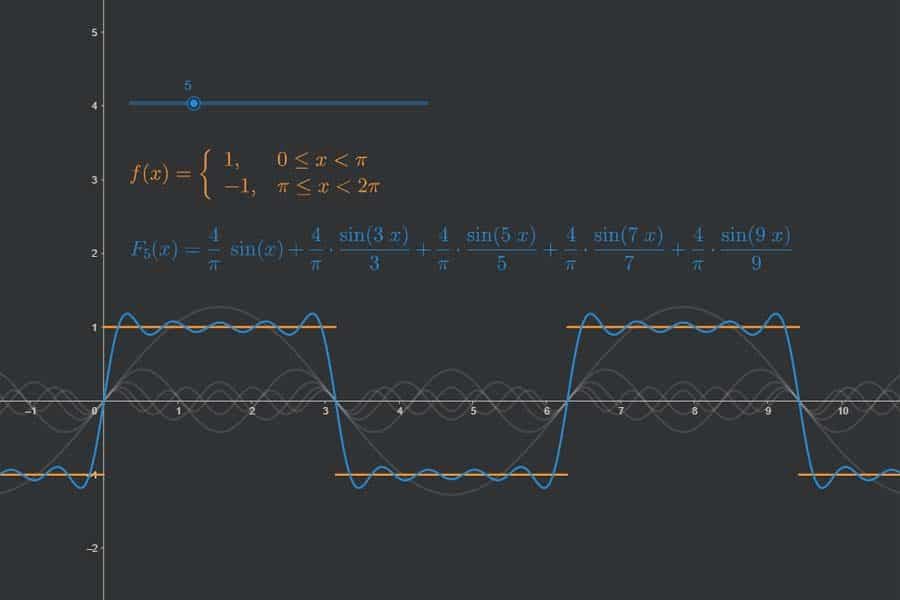
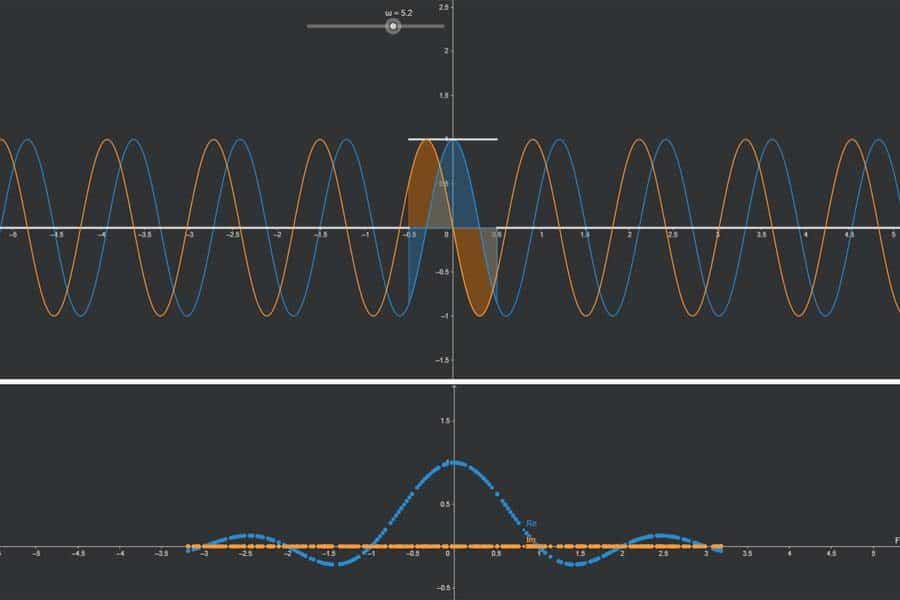
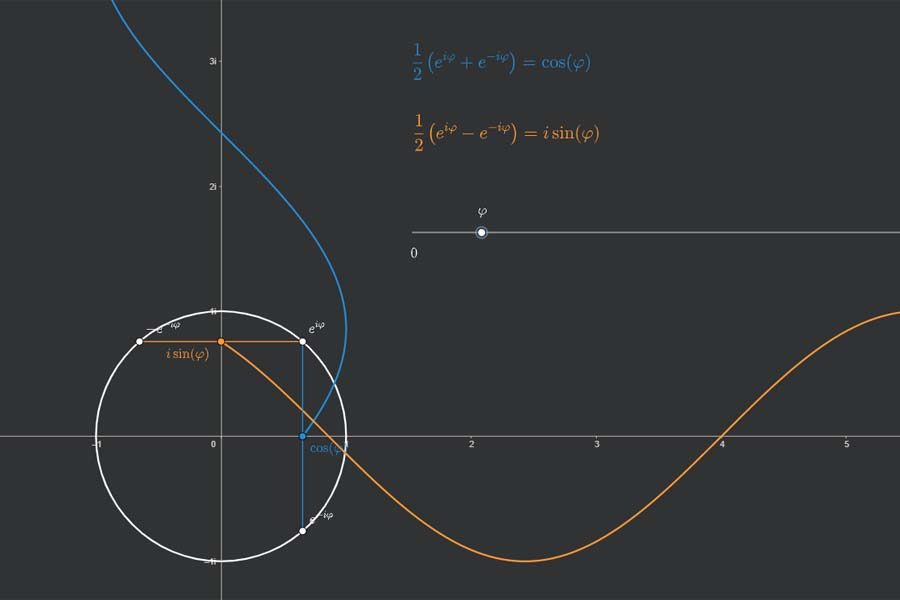
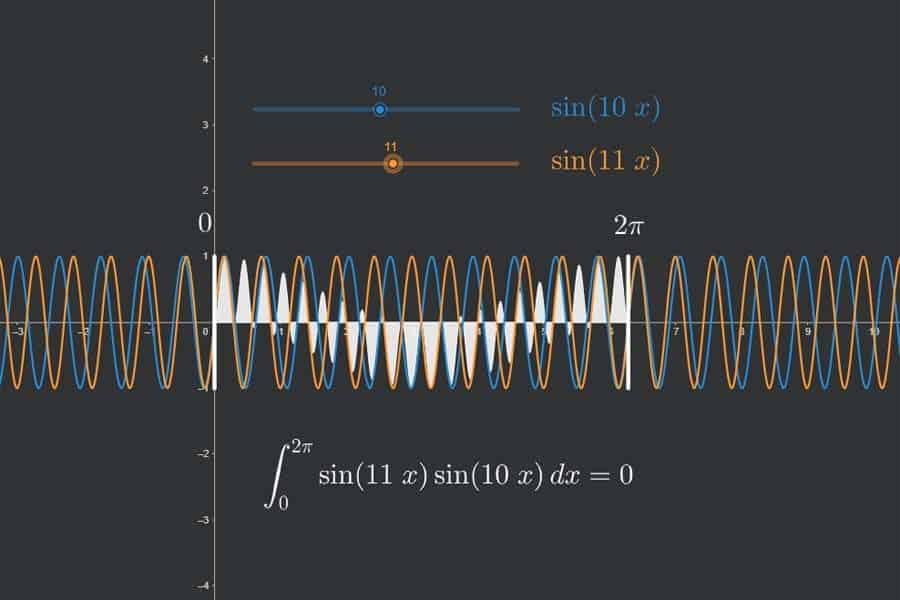
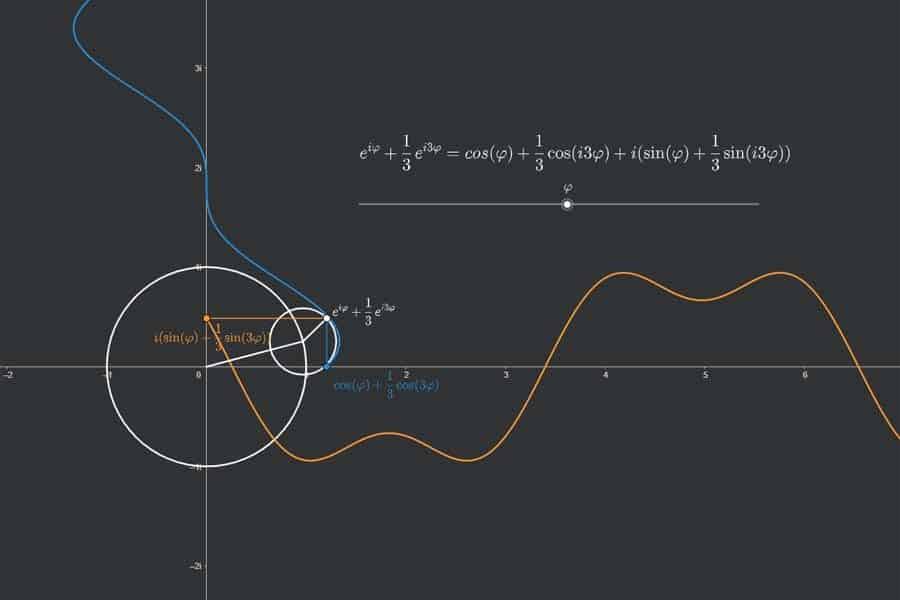
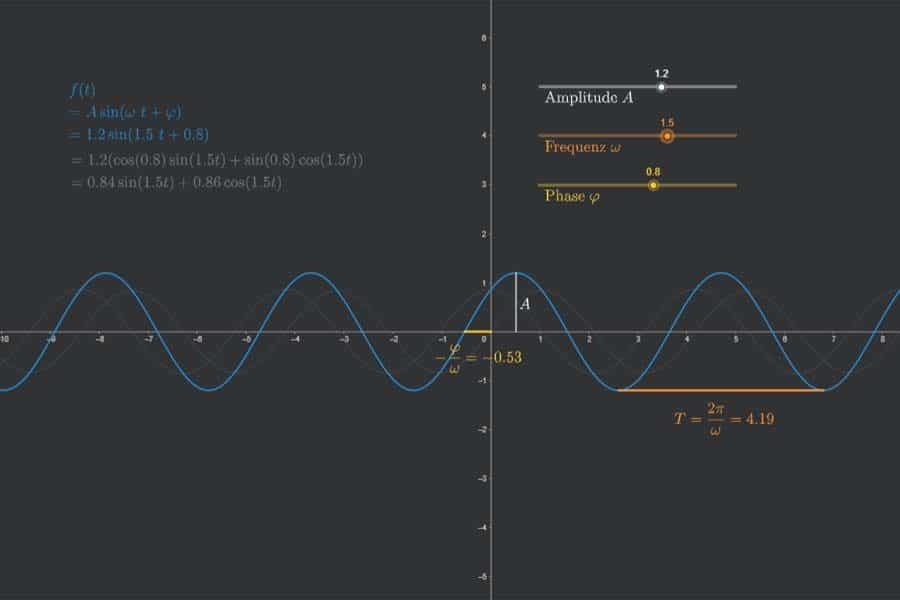
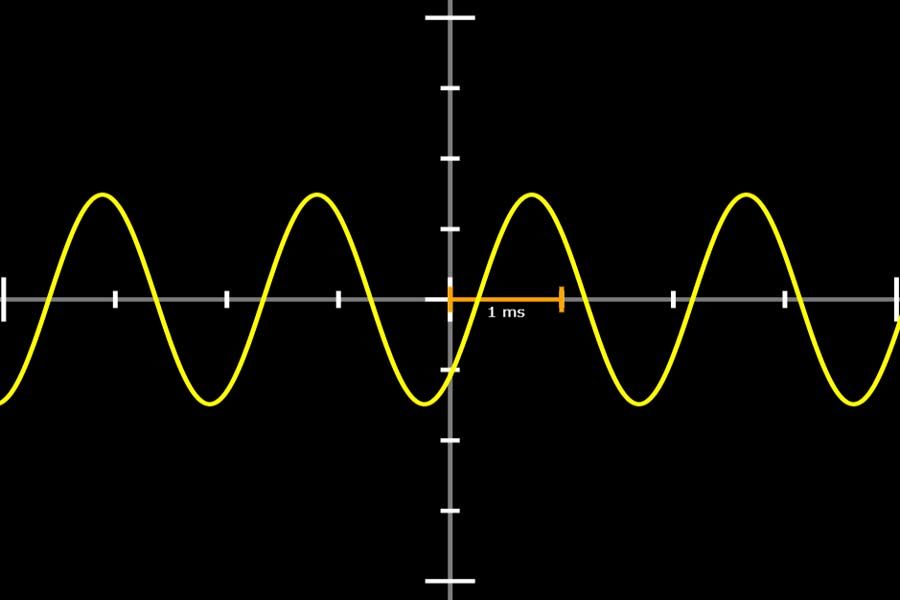
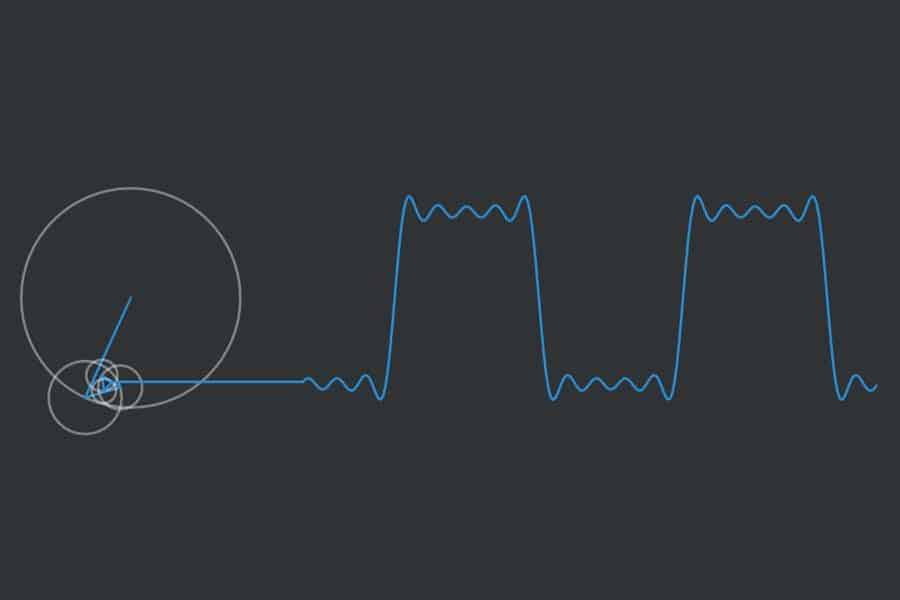
Interaktiv: Fourier-Synthese