Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Man kann die Fourier-Reihe von beliebigen Funktionen (hier: Rechtecksfunktion) von so genannten Epizykeln zeichnen lassen, das sind Kreise, die auf Kreisen sitzen, die auf Kreisen sitzen…


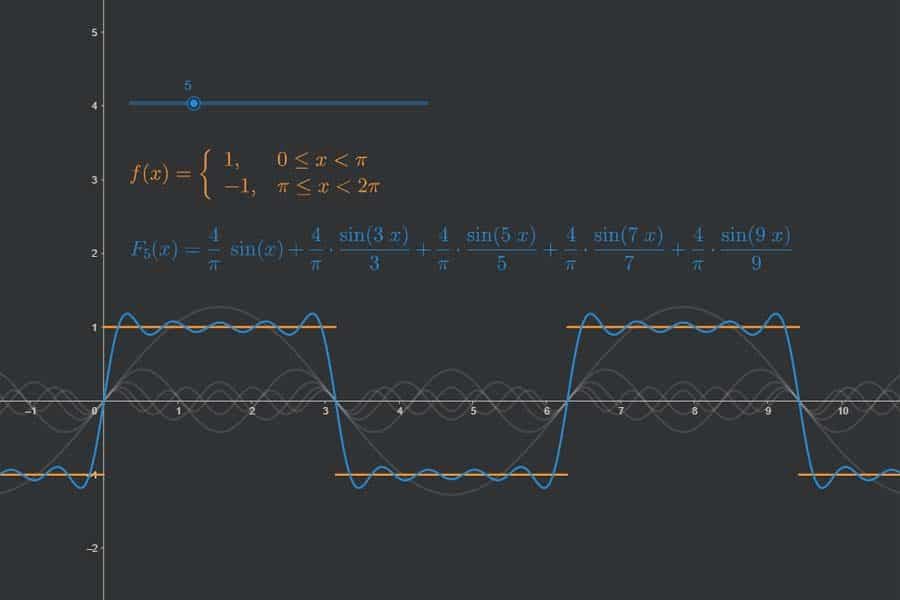
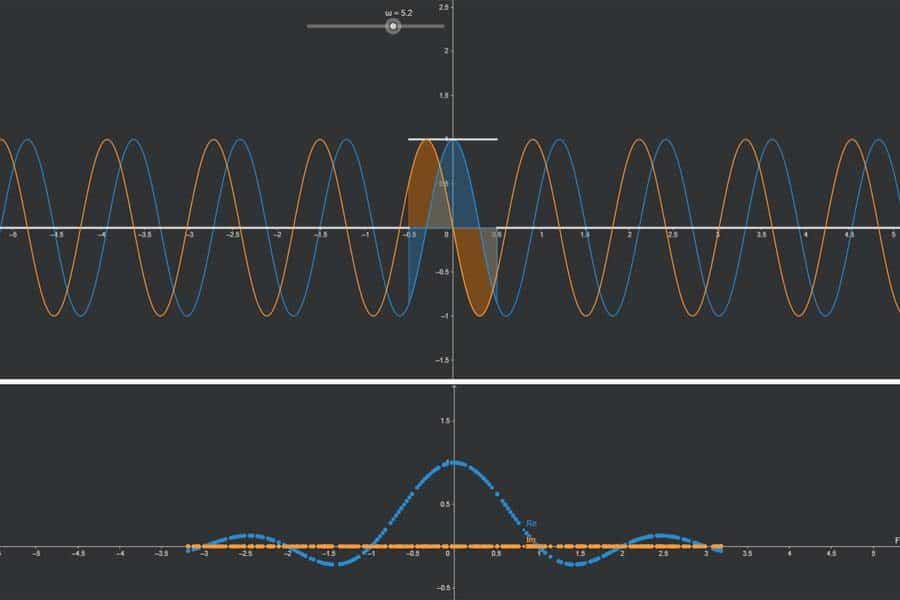
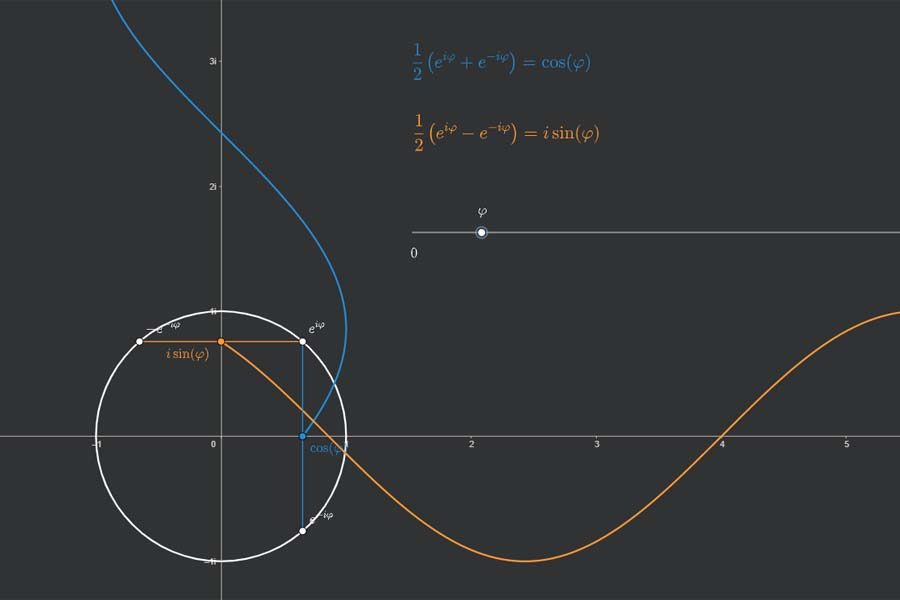
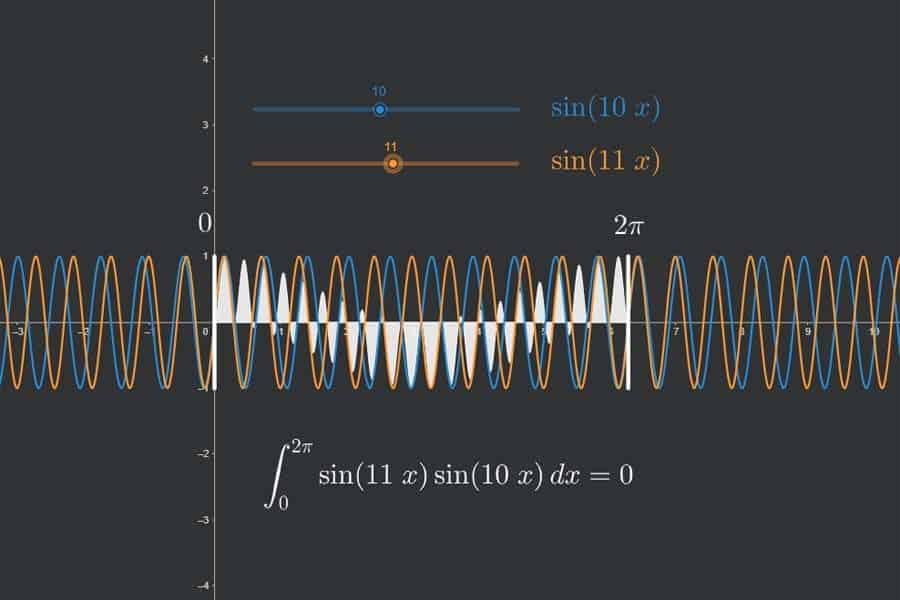
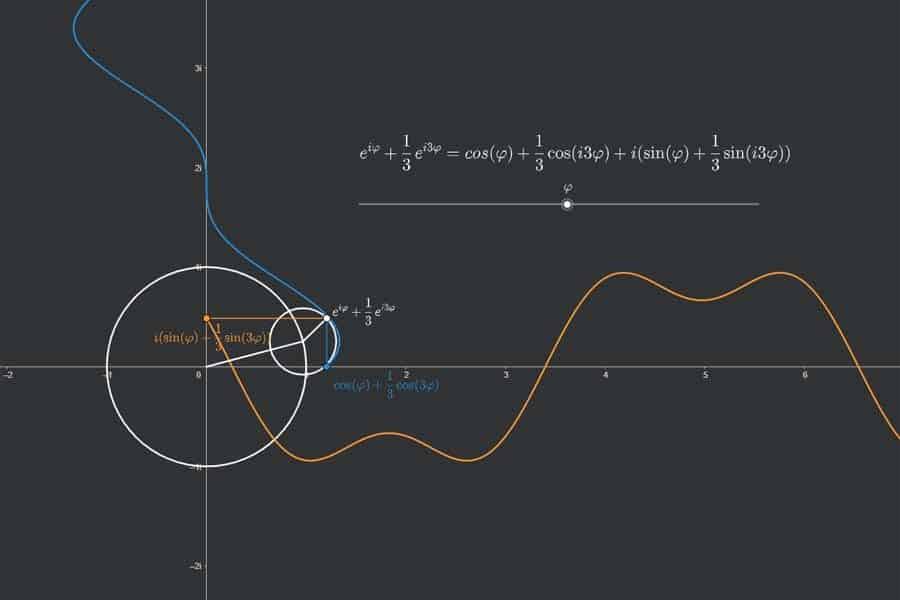
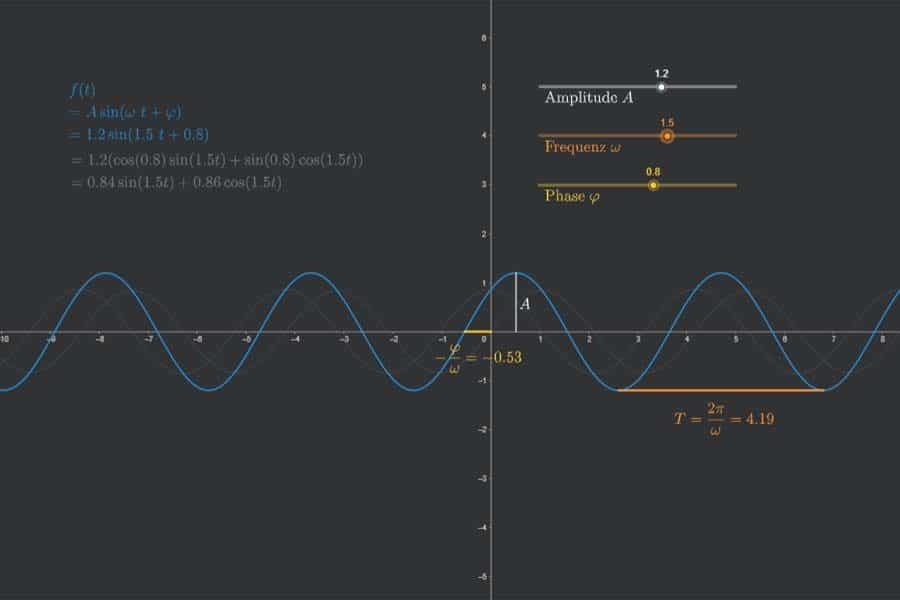
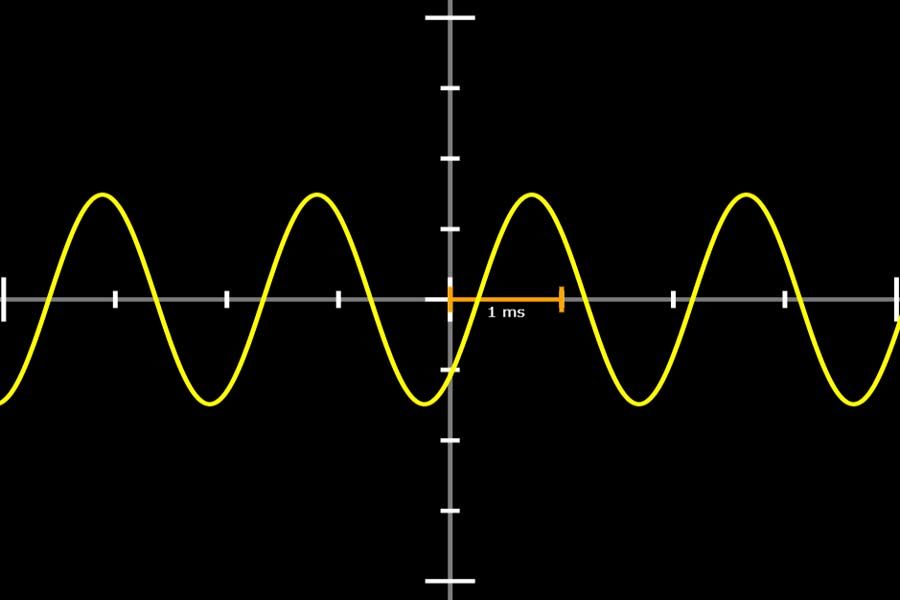
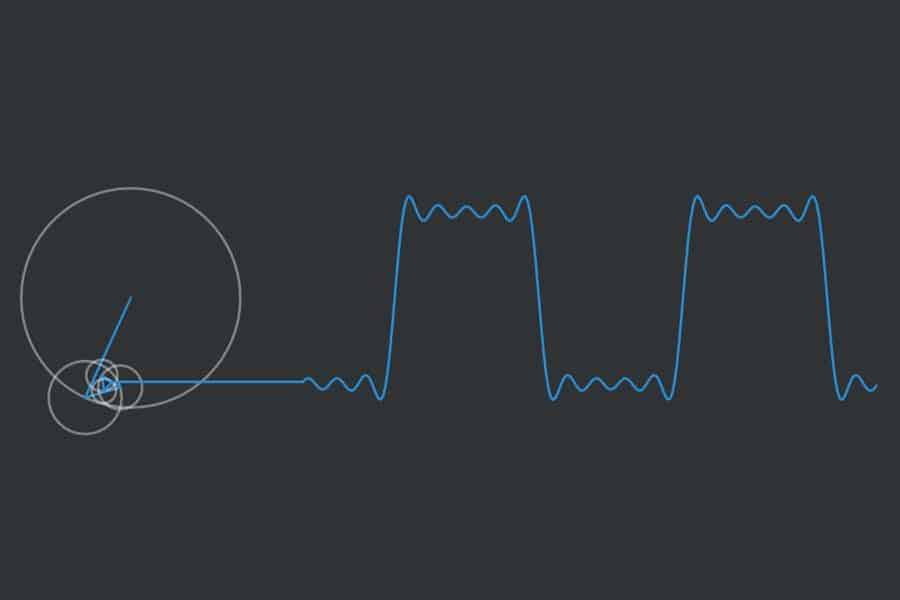












Interaktiv: Fourier-Synthese