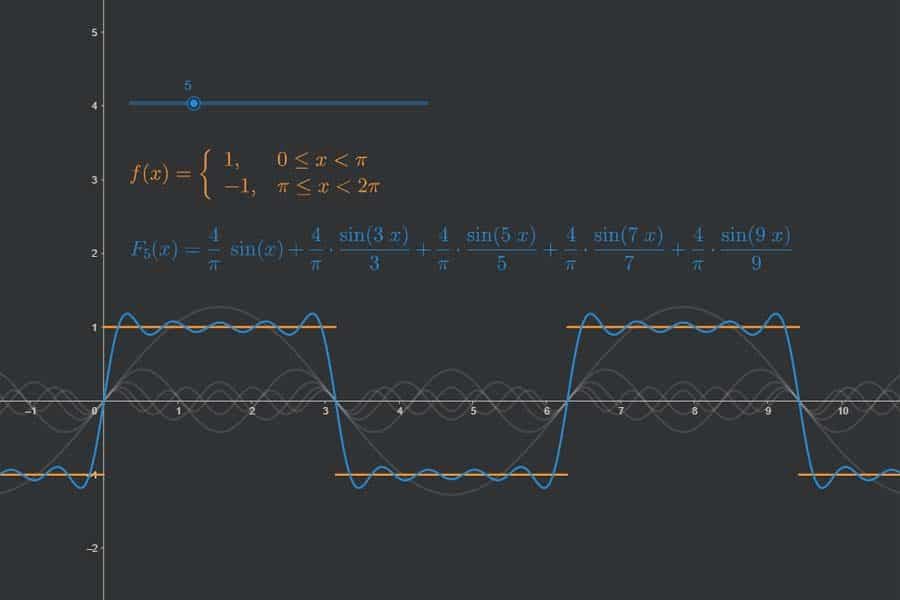
Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
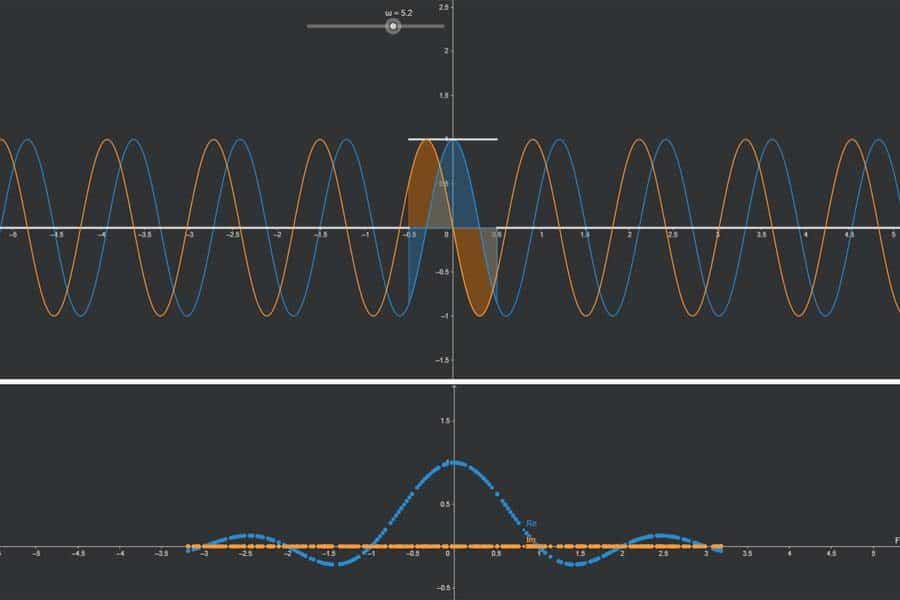
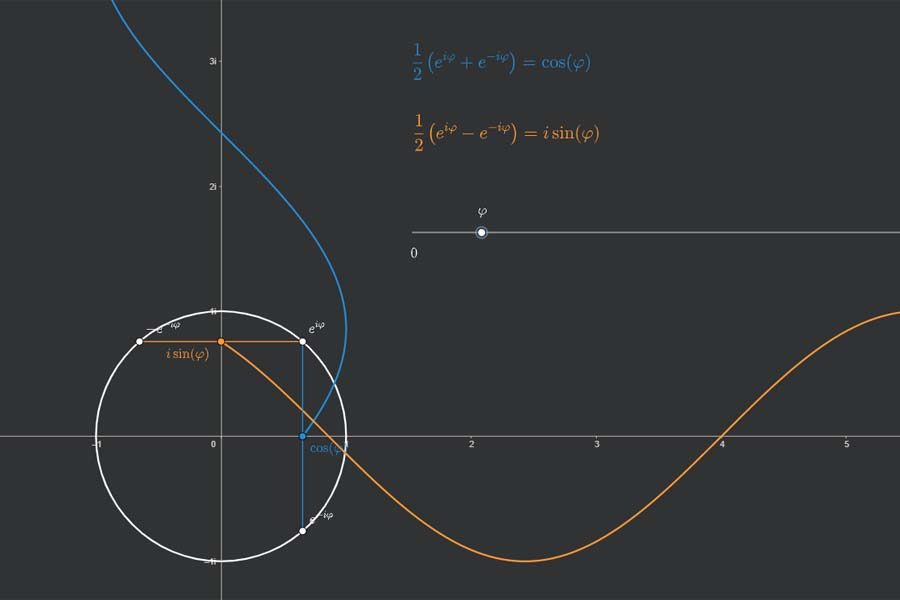
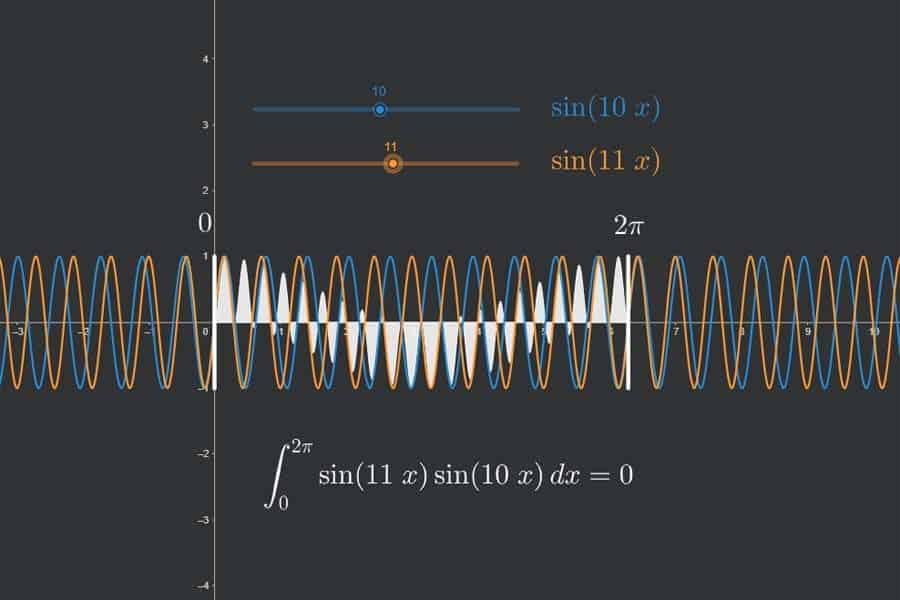
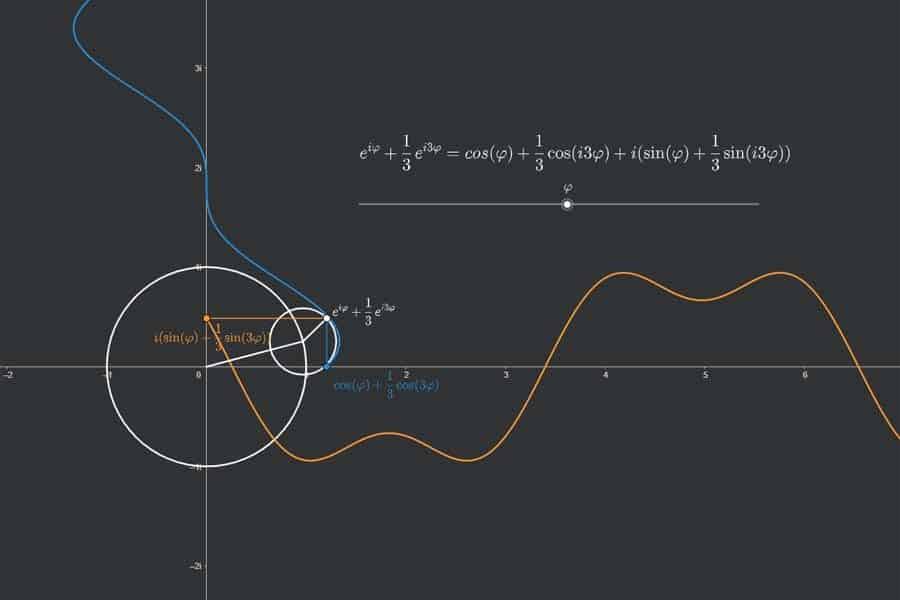
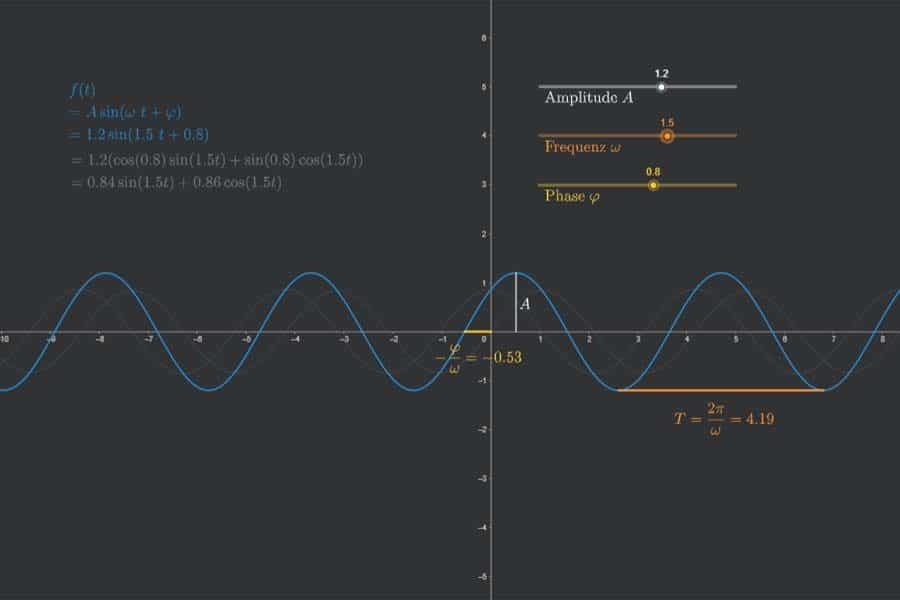
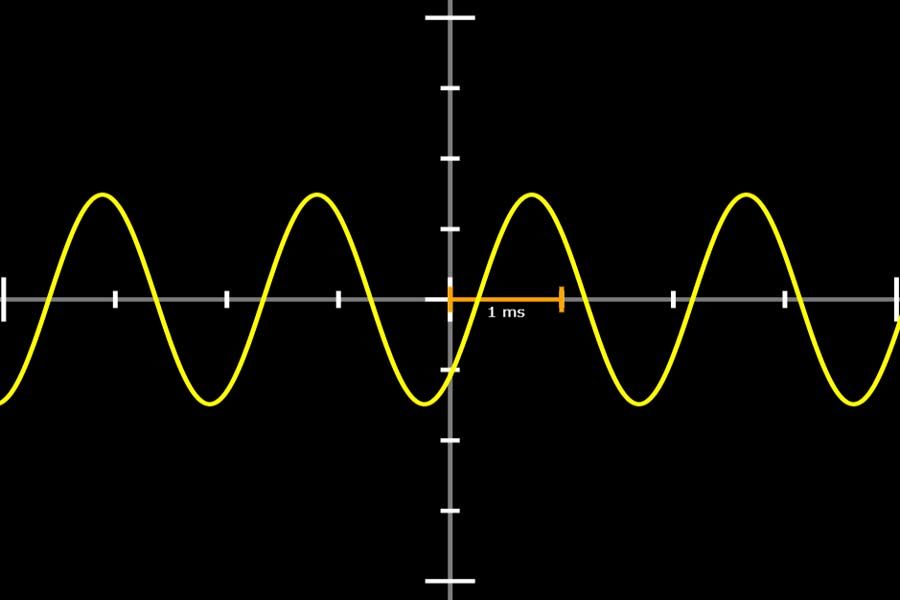
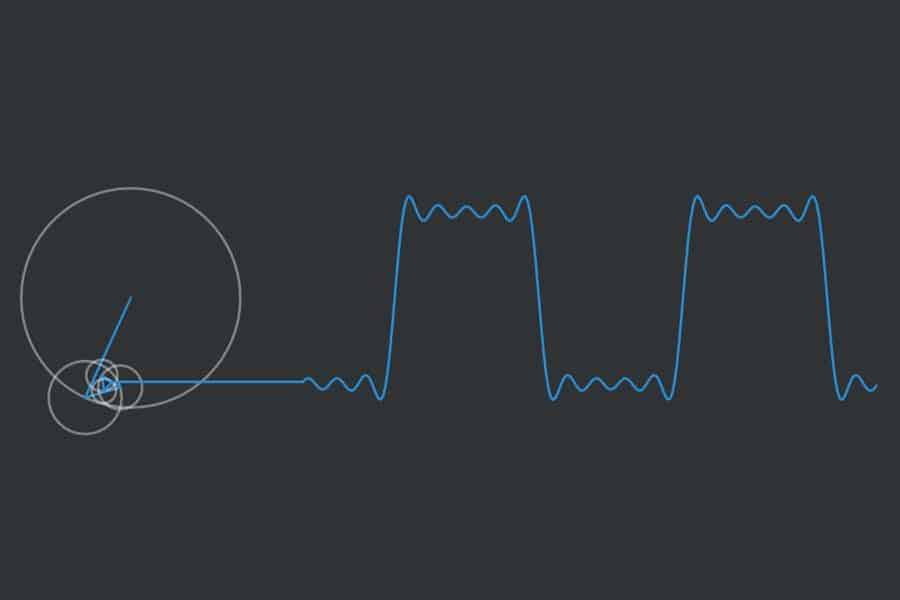
Die Fourier-Transformation wandelt eine gegebene Funktion in zwei neue Funktionen um: „Realteil“ und „Imaginärteil“. Diese beiden Funktionen kann man auffassen als Lautstärkeangaben für die Sinus- und Kosinusschwingungen verschiedener Frequenzen, aus denen die Originalfunktion zusammengesetzt ist – der Realteil für Kosinusanteile, der Imaginärteil für Sinusanteile. Somit übersetzt die Fourier-Transformation die Funktionen aus der „Zeit-Welt“ in die „Frequenz-Welt“. In der App wird eine einfache achsensymmetrische Funktion transformiert (Puls-Funktion). Diese haben nur Kosinusanteile (blau). Die Sinusanteile (orange) sind alle null.














Interaktiv: Fourier-Synthese