Die Sinusfunktion kennt man ja. Ihr Schaubild sollte jeder mal eben skizzieren können. Sie hat ihre Nullstellen bei den ganzzahligen Vielfachen von π, also z. B. 0, -π, π, 2π usw., und schwingt wunderbar hin und her. Aber: Es gibt sie auch in verallgemeinerter Form, d.h. verschoben, gequetscht, gestreckt oder gestaucht, oder alles zusammen.
Bewege die drei Schieberegler, für die allgemeine Sinusfunktion f(x) ihre Amplitude A („Lautstärke“), ihre Frequenz ω („Tonhöhe“) und den so genannten Phasenwinkel φ zu verändern. Beobachte dabei, wie sich der Graph von f verändert. Die Periode T von f verhält sich antiproportional zur Frequenz ω: Wenn sich die Frequenz verdoppelt, dann halbiert sich die Periode und anders herum. Mit Hilfe des Additionstheorems für Sinus und Kosinus lässt sich die allgemeine Sinusfunktion in eine Linearkombination einer Sinus- und eine Kosinusfunktion gleicher Frequenz zerlegen (grau dargestellt). Dieser „Mix“ aus Sinus- und Kosinusschwingung wird im Wesentlichen durch den Phasenwinkel φ bestimmt.
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Fourier-Reihe der Rechteckfunktion? Hart? Auf jeden Fall. Hier wird's veranschaulicht.
Fourier-Transformation zum Leben erweckt. Jetzt wird's endlich klar...
Sinus und Kosinus im Gewand der komplexen Exponentialfunktion. Exotisch.
Sinusschwingungen verschiedener Frequenz multipliziert verhalten sich komisch.
Ein Kreis, der sich auf einem Kreis dreht. Abgedreht. Muss man auf sich wirken lassen.
Sinus und Kosinus: Wir stauchen, schieben und strecken sie hart. Und Trocken.
Come on crazy party people make some noise! Lautsprecher an und los geht's!
Kreise sitzen auf Kreisen, die auf Kreisen sitzen, die auf Kreisen sitzen, die auf...
Zeichne eine beliebige Figur und lasse sie nachzeichnen von Kreisen, die auf Kreisen sitzen.
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
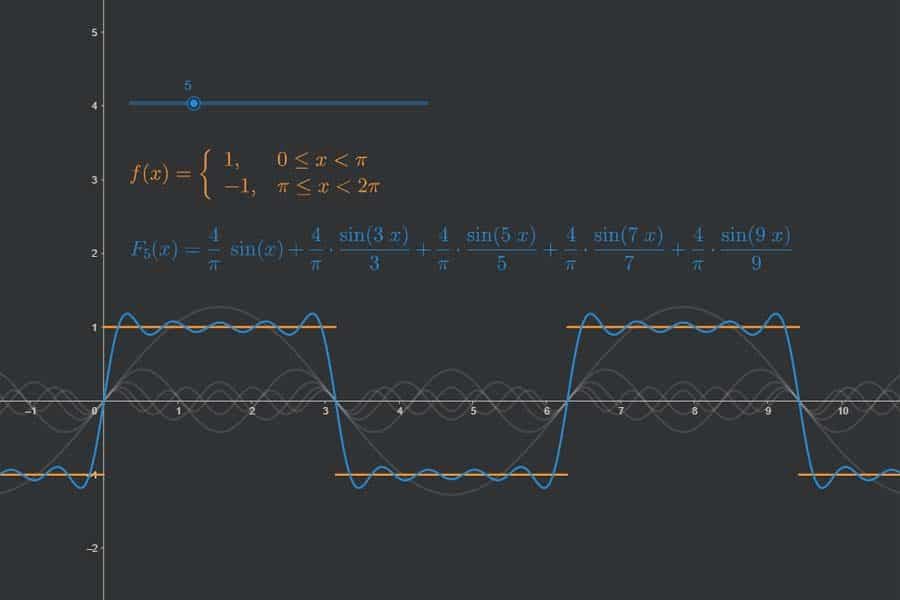
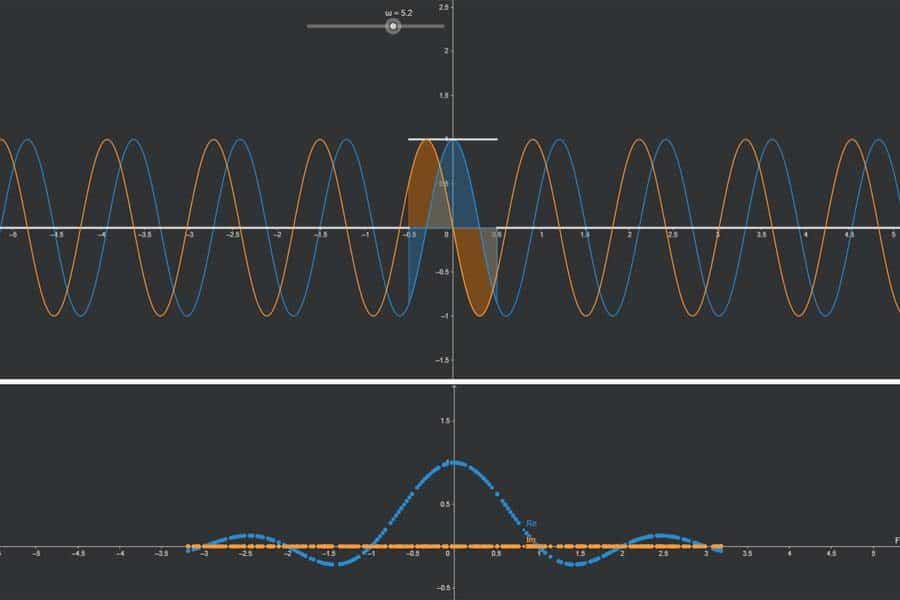
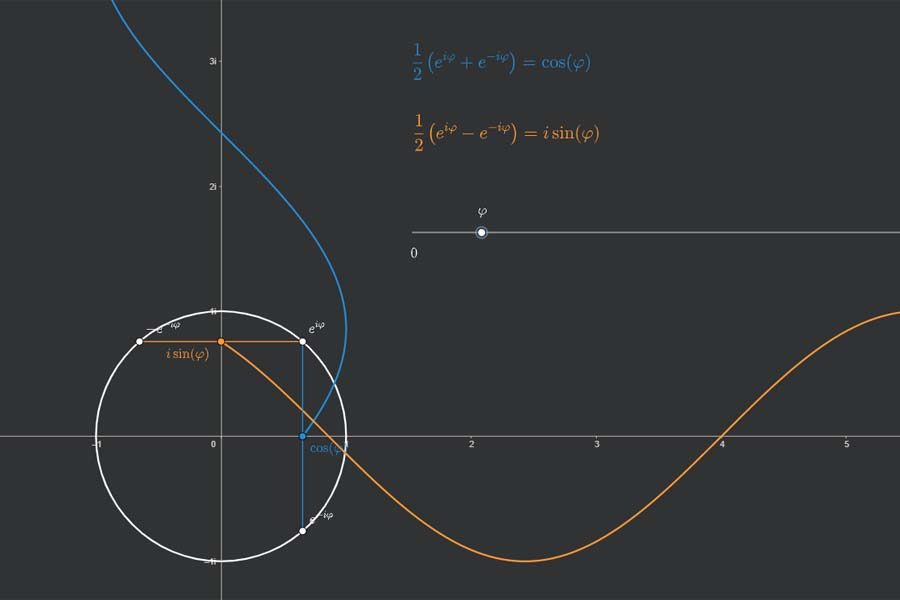
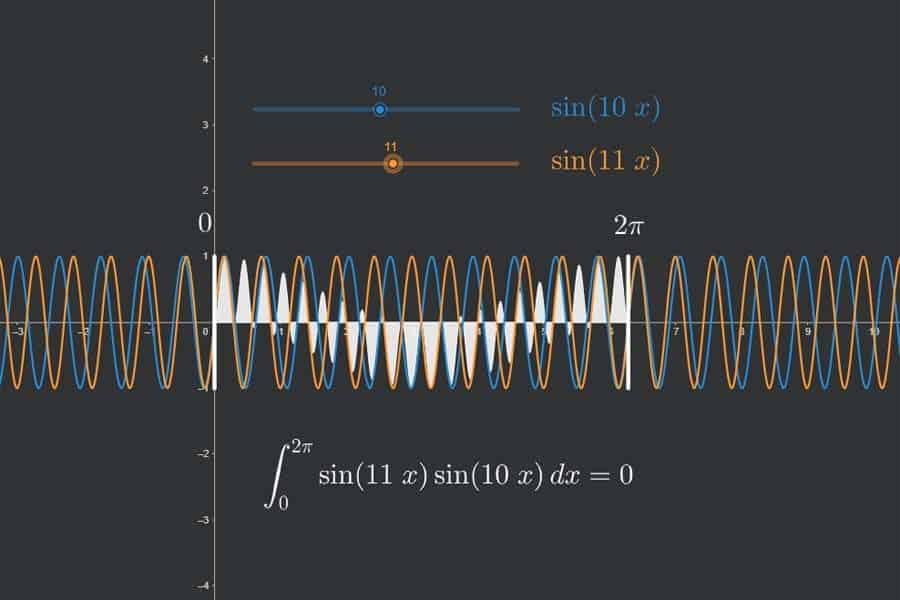
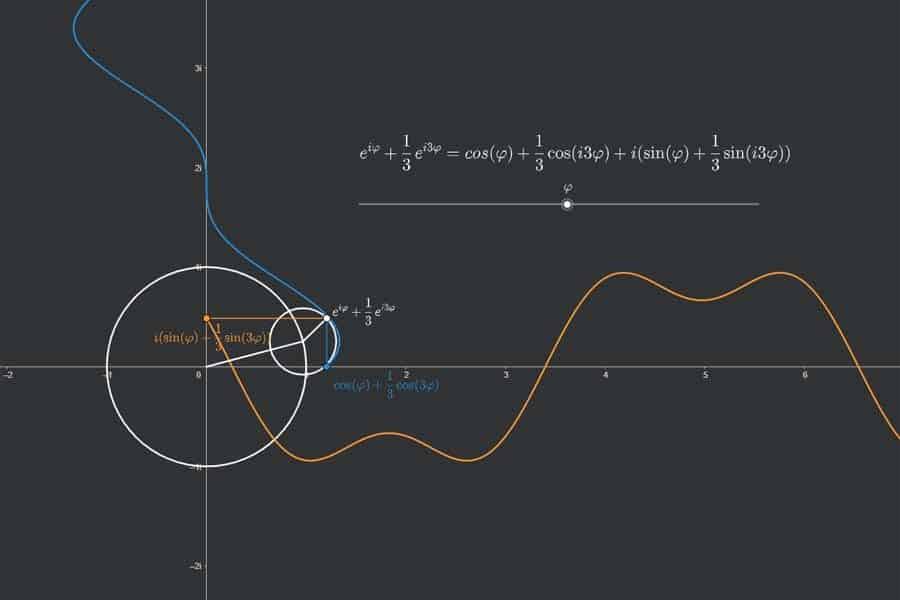
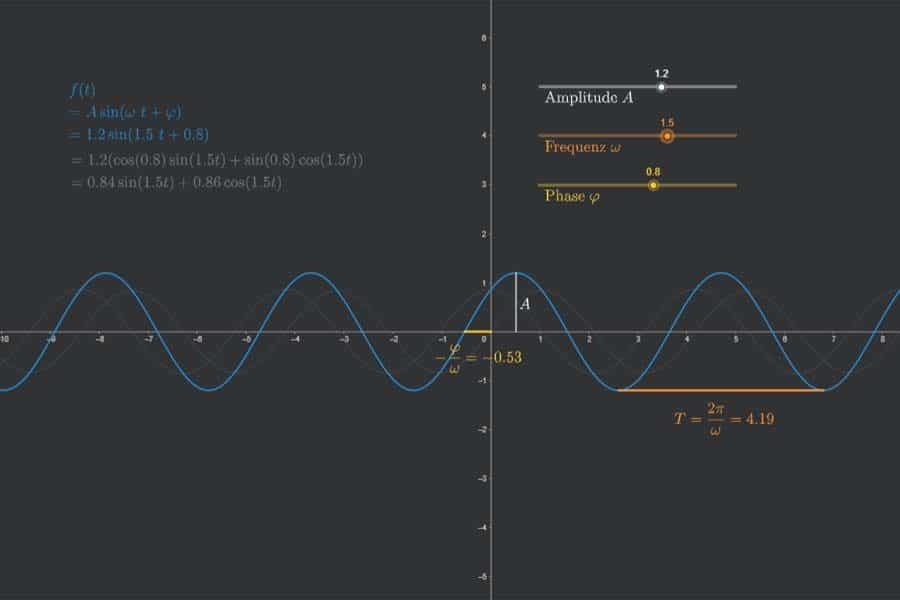
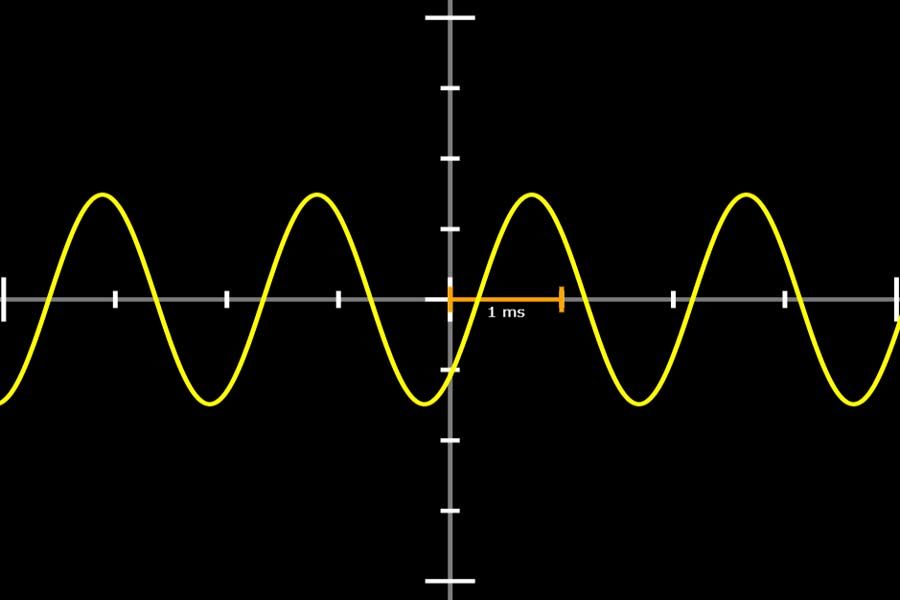
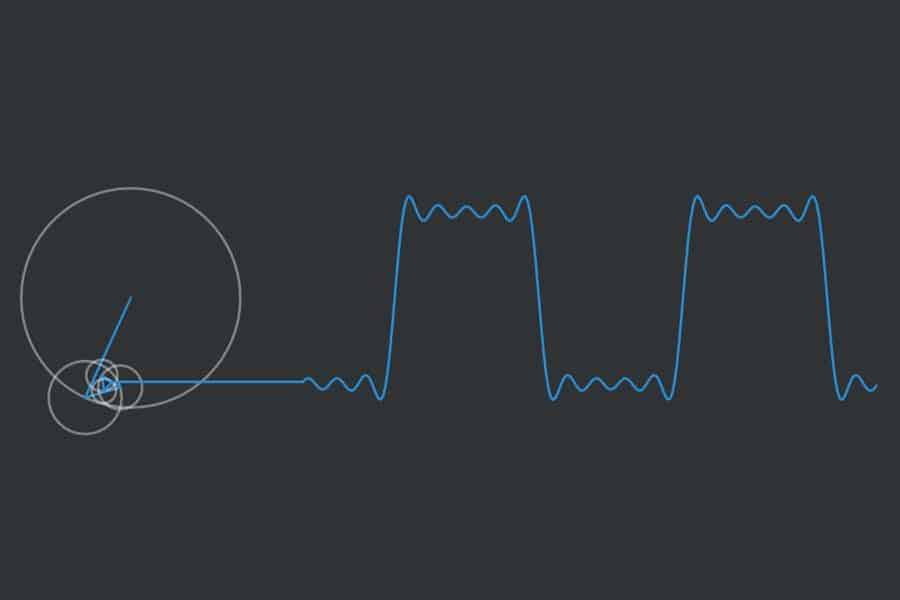
Interaktiv: Fourier-Synthese