Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
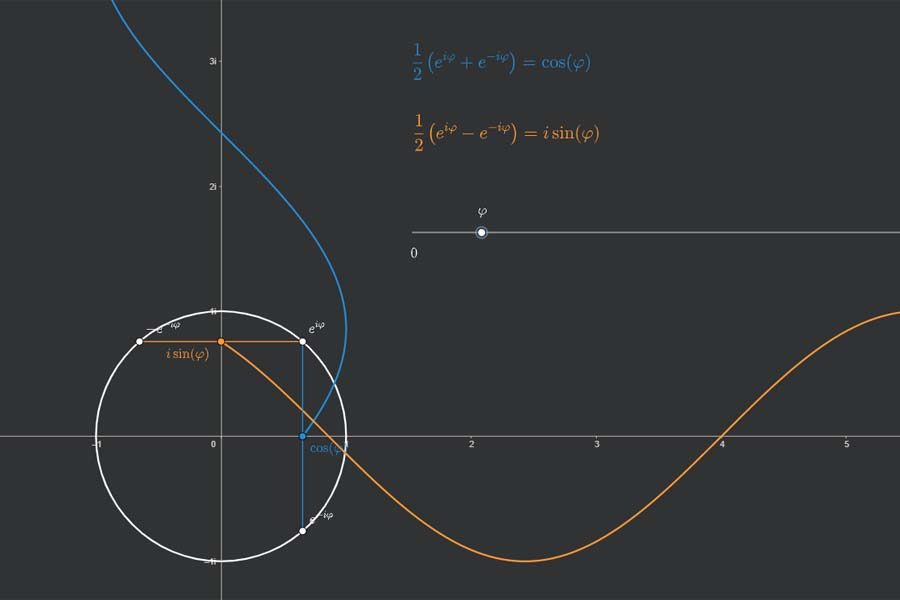
Wer die „komplexe Exponentialfunktion“ (will heißen: die Exponentialfunktion erweitert auf komplexe Zahlen) kennt, der kennt auch die Eulersche Gleichung, die sagt, dass exp(iφ)=cosφ+ i sinφ ist. Sie hilft dabei, Gleichungen zu finden, die den handelsüblichen Sinus bzw. Kosinus über die komplexe Exponentialfunktion ausdrücken, was z. B. nützlich ist, wenn man die reelle Fourier-Reihe in komplexer Form ausdrücken will.


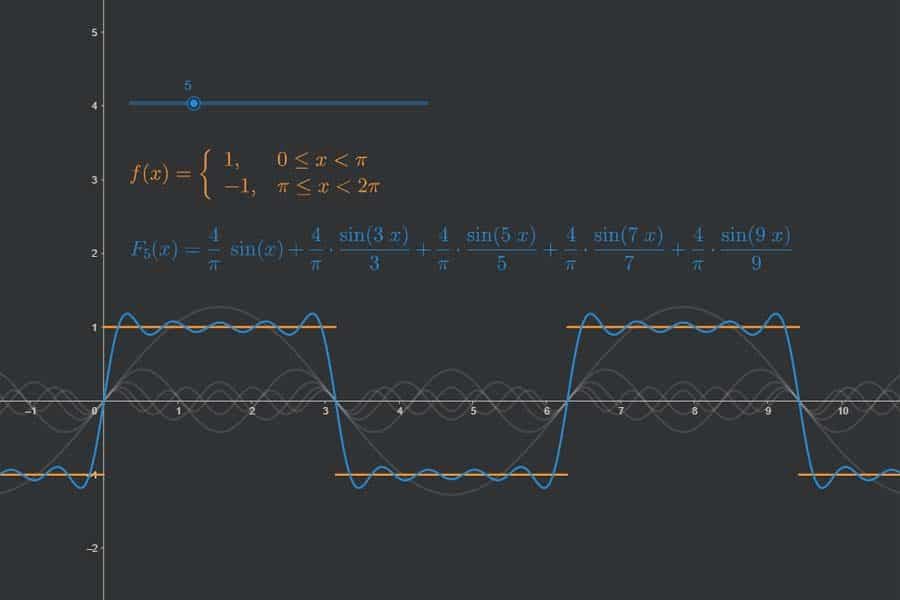
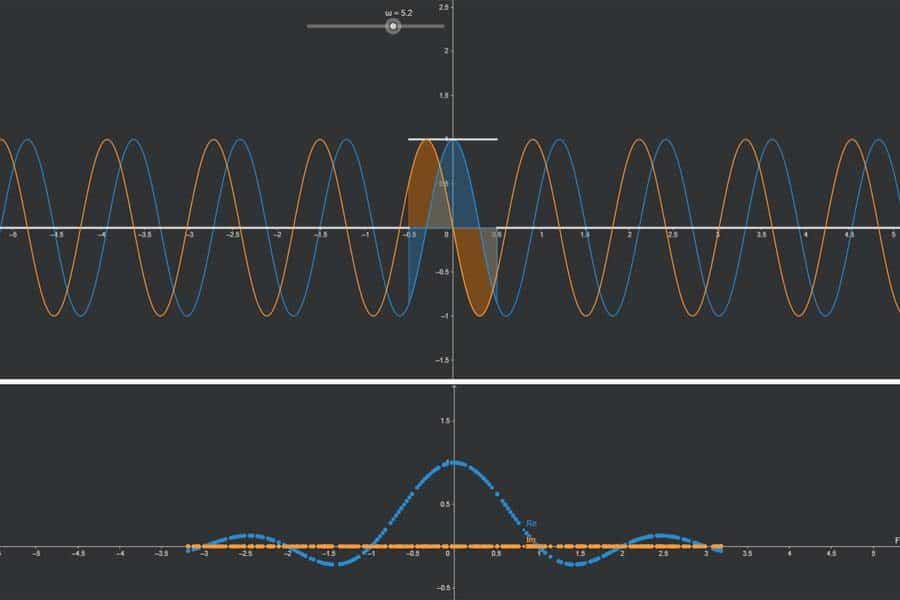
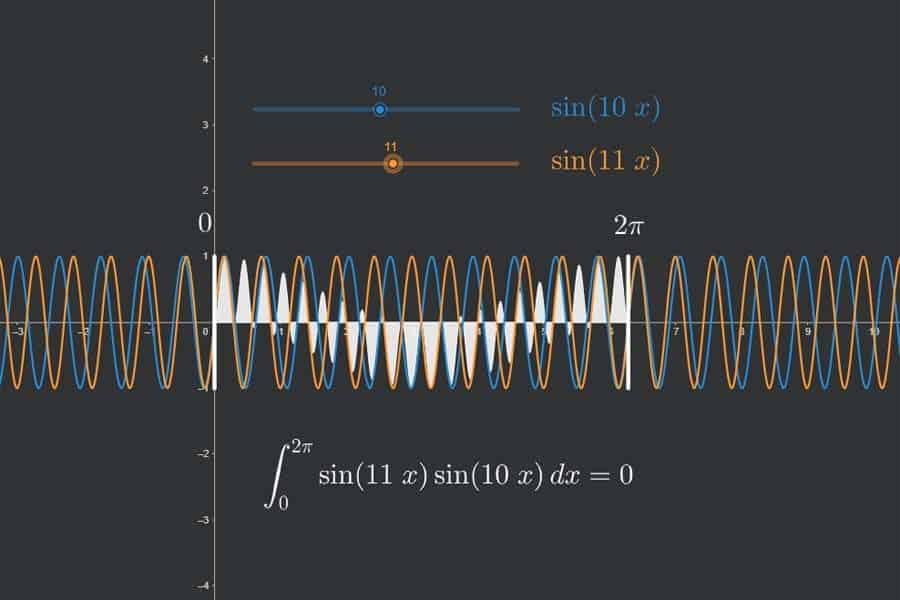
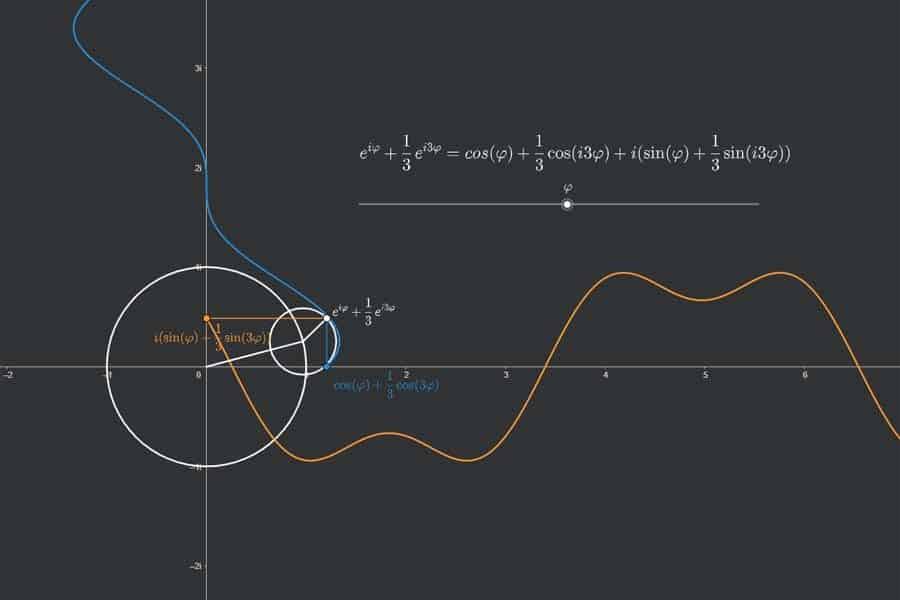
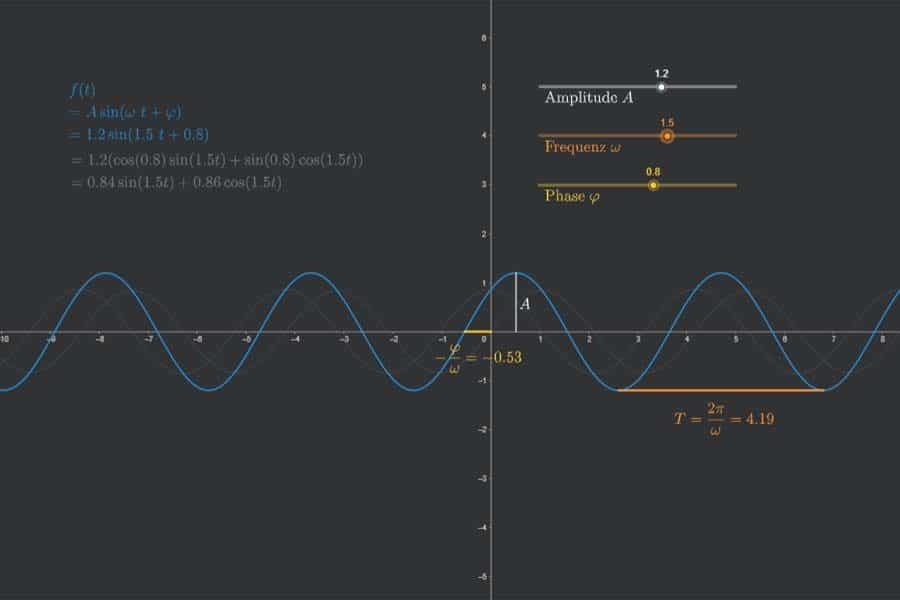
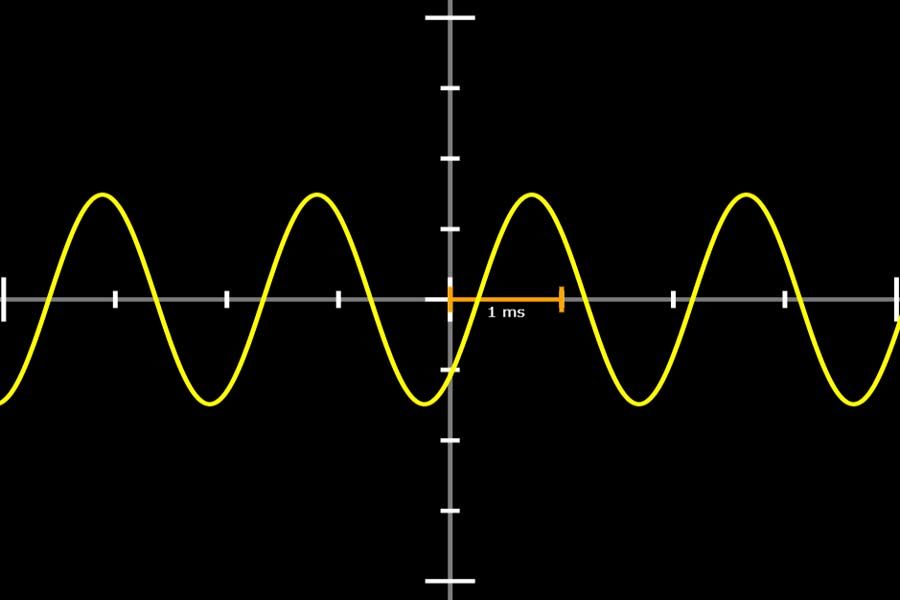
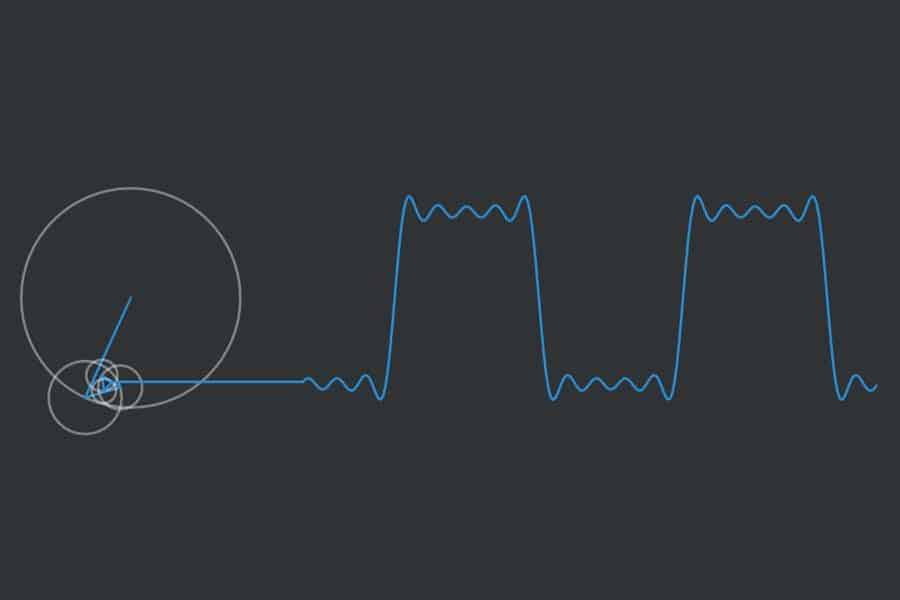












Interaktiv: Fourier-Synthese