Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Wie kann man Sinus- und Kosinusschwingungen gleicher Frequenz und Amplitude kombinieren? Man schaut sich einen Punkt an, der sich mit konstanter Geschwindigkeit auf einer Kreislinie bewegt. Seine vertikalen Bewegungen bilden eine Sinus-, seine horizontalen Bewegungen eine Kosinusschwingung. Wenn jetzt mehrere solcher Schwingungen mit verschiedenen Frequenzen kombiniert (addiert) werden, dann setzt man auf diesen Punkt auf der Kreislinie einen weiteren Kreis und betrachtet einen Punkt, der sich auf diesem Kreis bewegt. Klingt kompliziert? Ist es auch. Daher genau hinschauen und am besten etwas drüber meditieren.


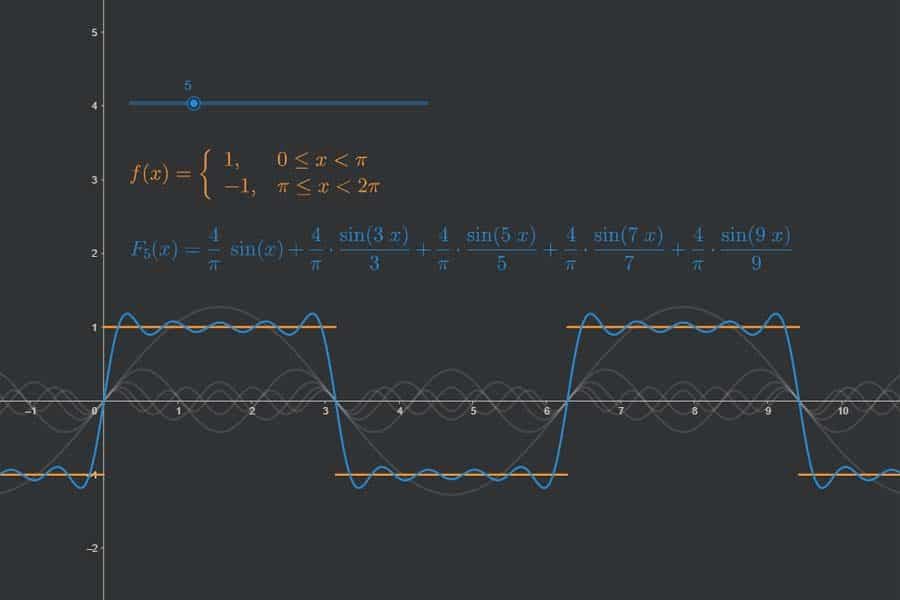
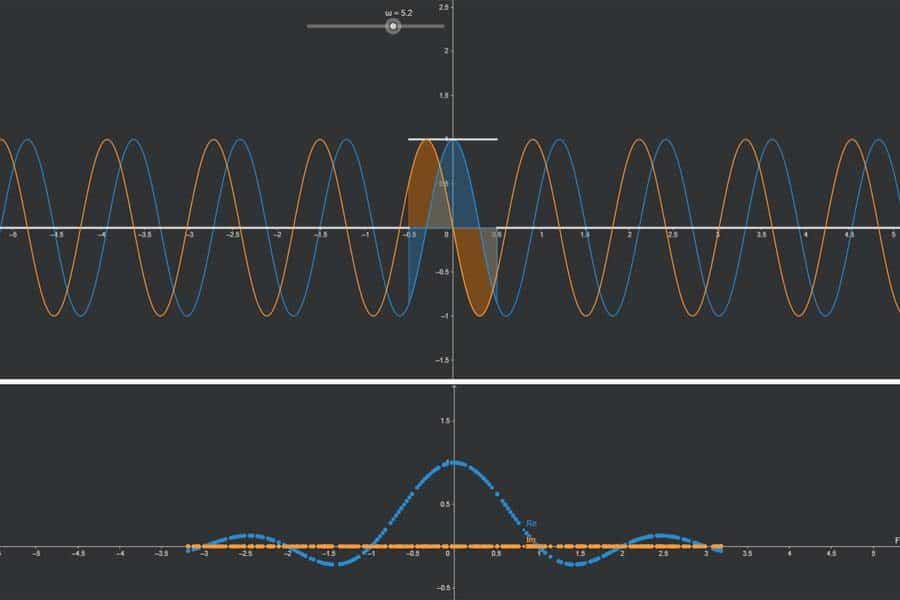
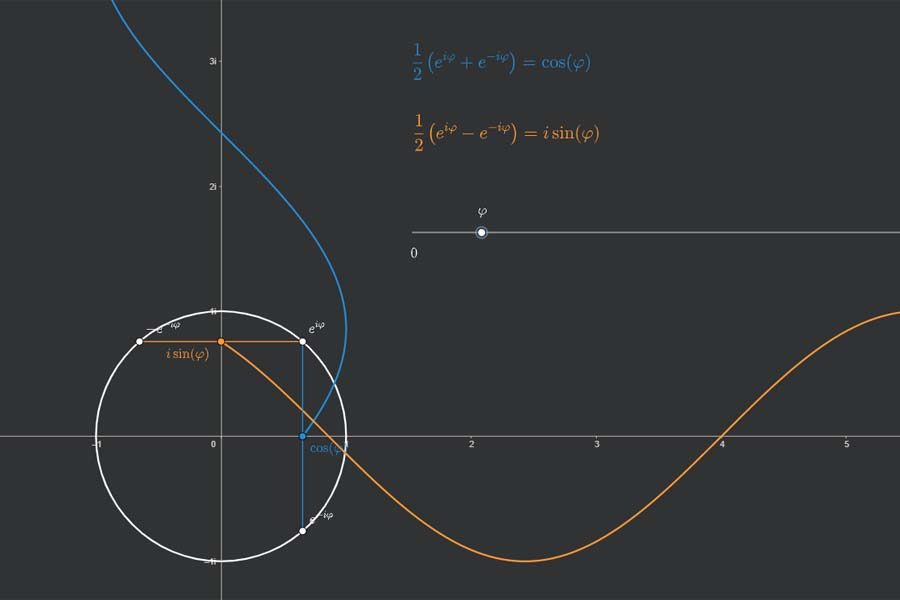
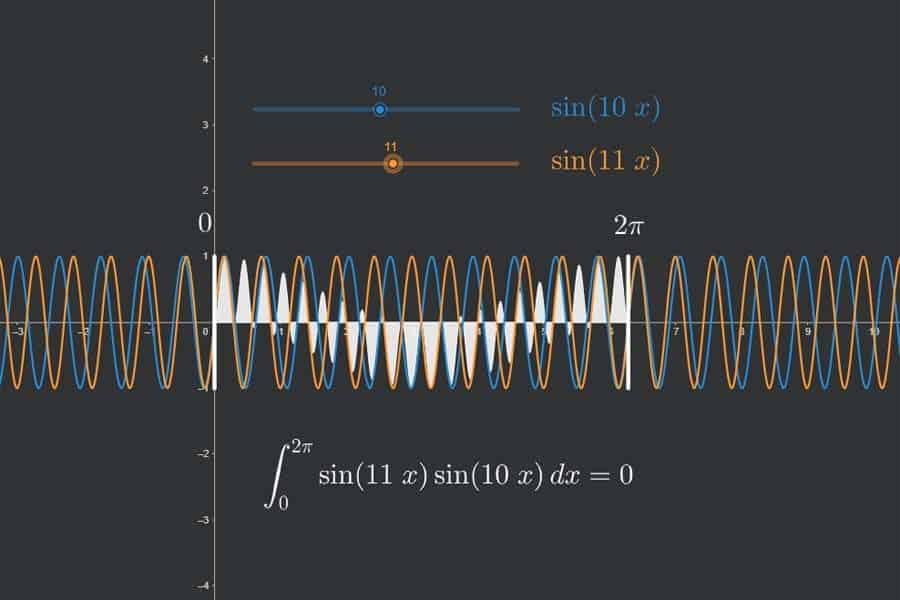
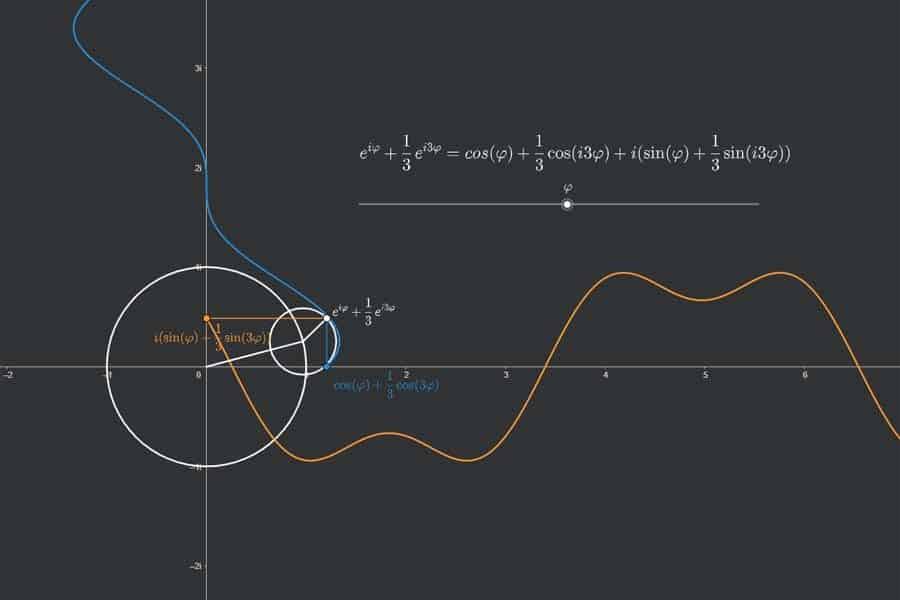
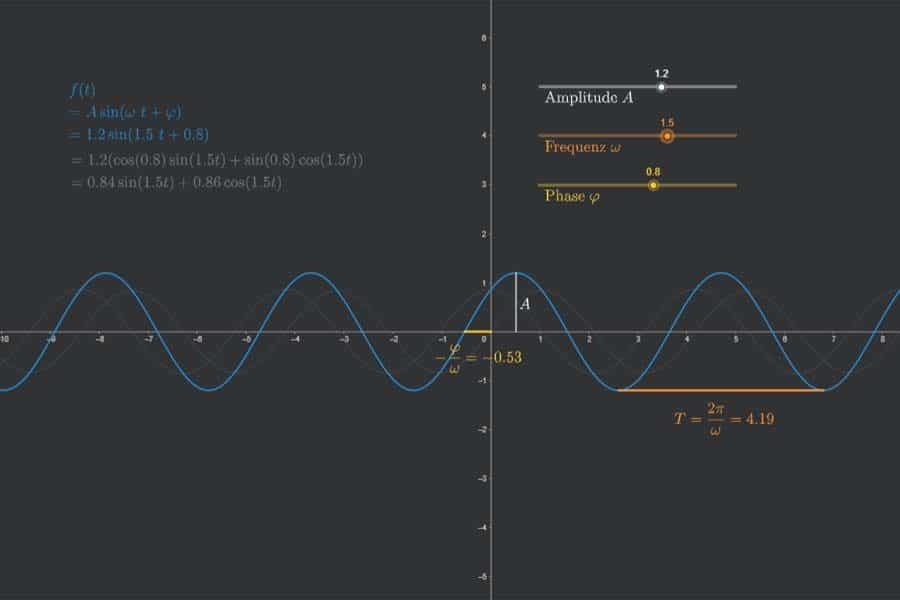
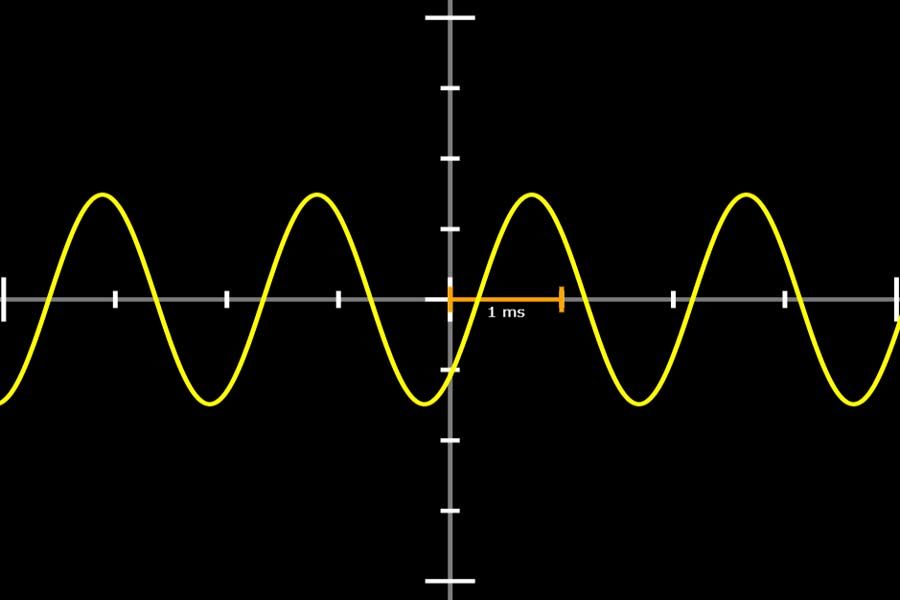
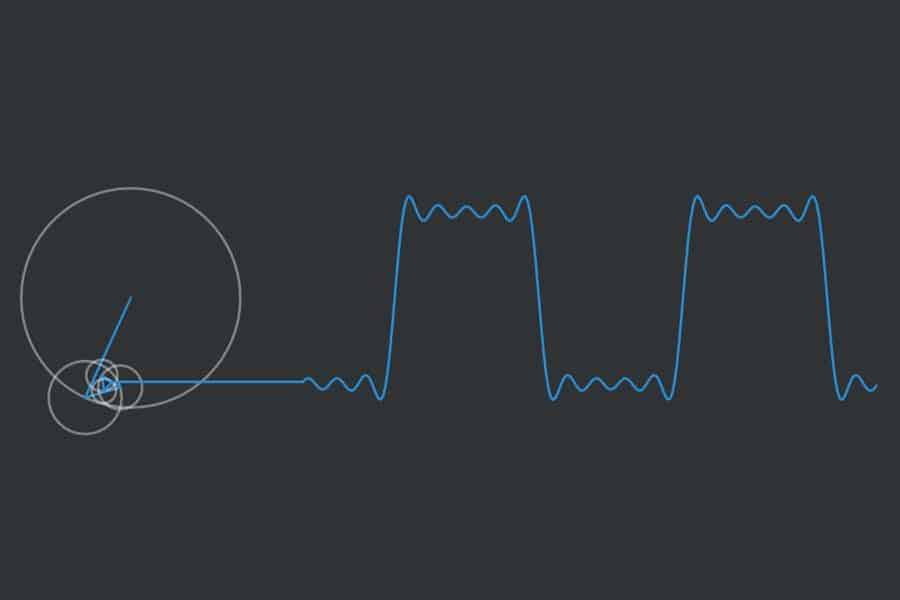












Interaktiv: Fourier-Synthese