Funktion in Spiegelschrift. Ableitung in Spiegelschrift. Mit Bild ist die Lösung so einfach.
Wenn man „Ableitung“ bzw. „differenzierbar“ genau denkt, dann kommt man immer zum Begriff der Folge und des Differentialquotients. Genauso, wie Folgen von links oder recht kommen können, kann man Differenzierbarkeit von links oder rechts definieren. Nur eines davon zu „haben“ ist immer weniger als „echte“ Differenzierbarkeit.


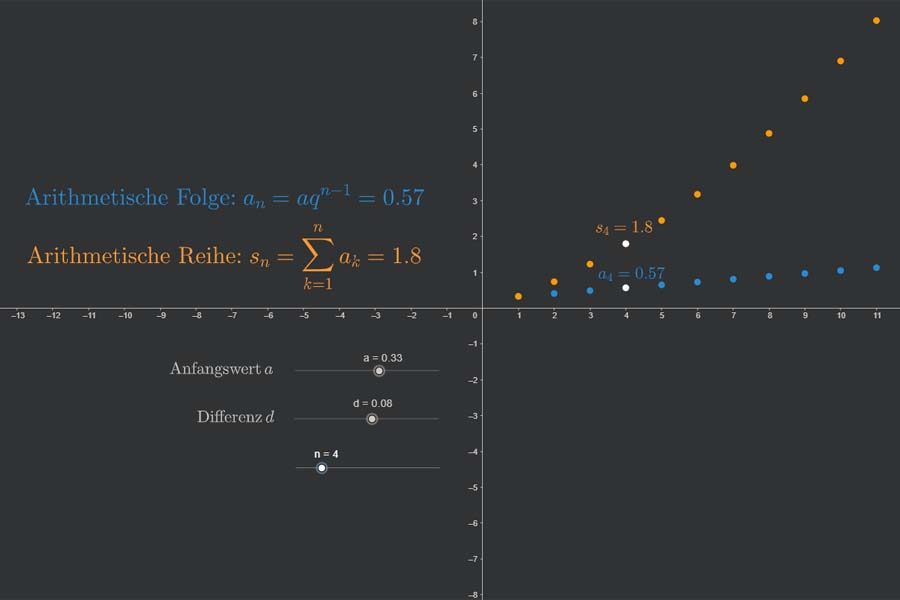
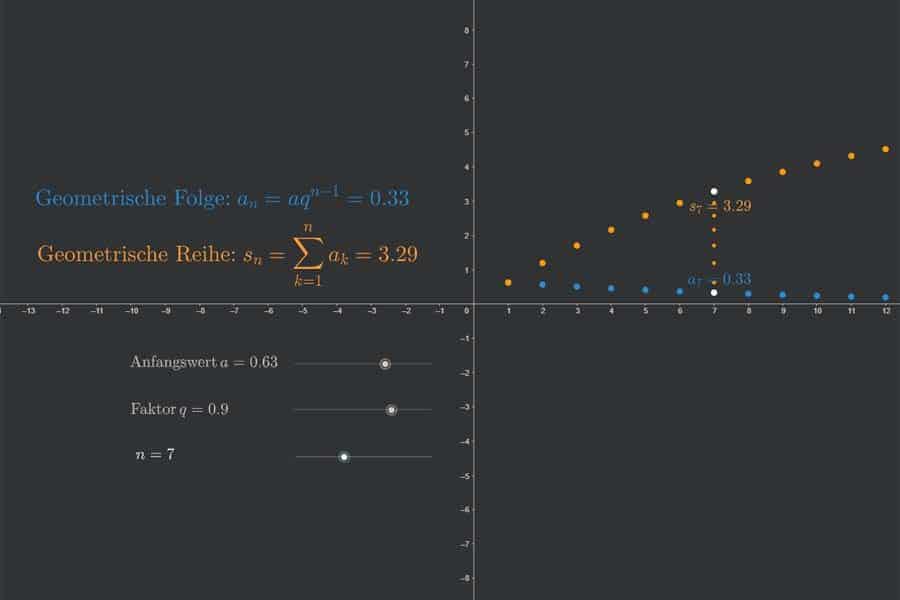
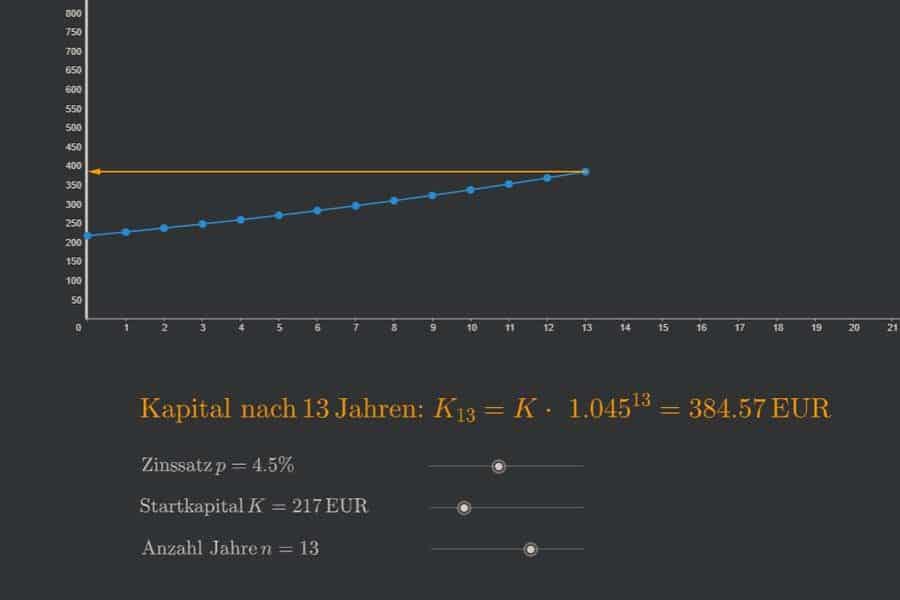
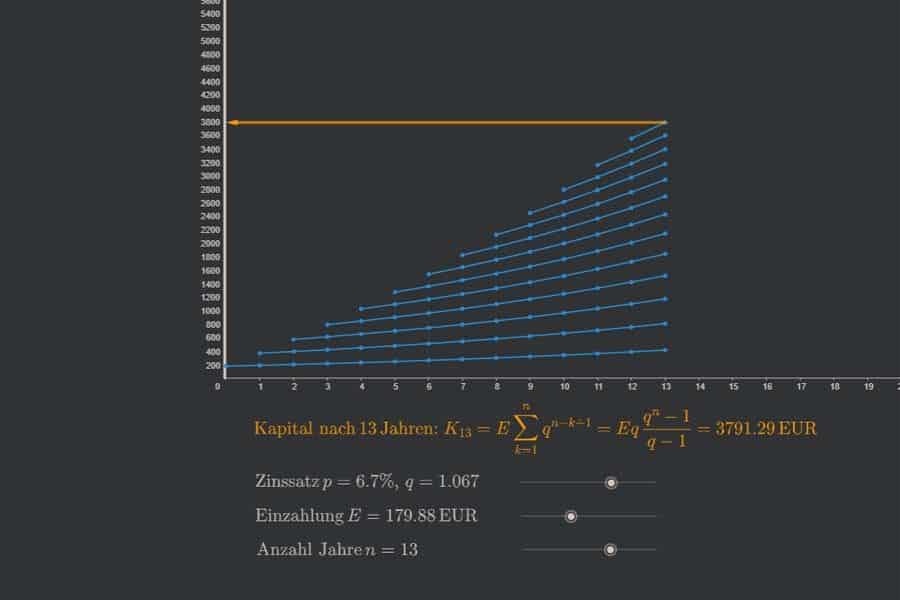
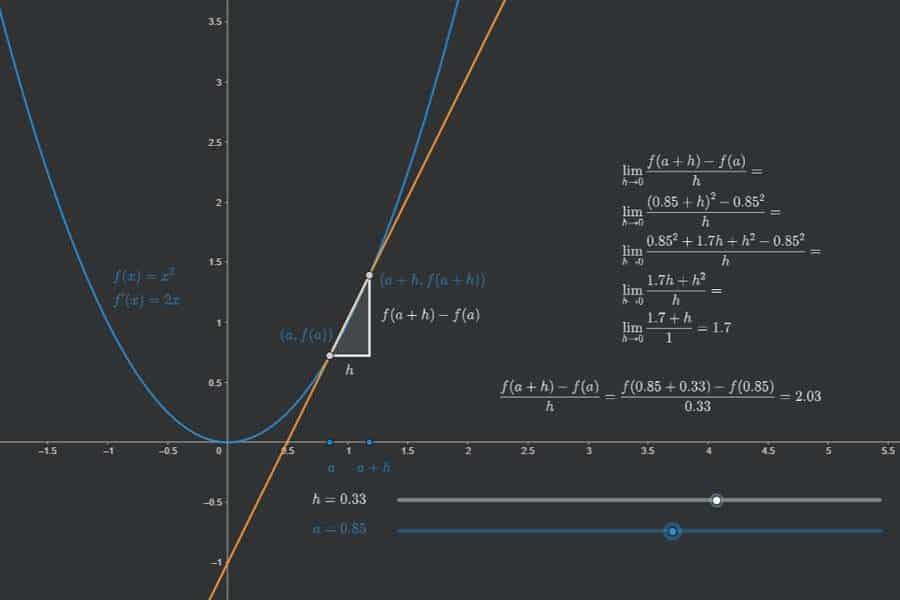
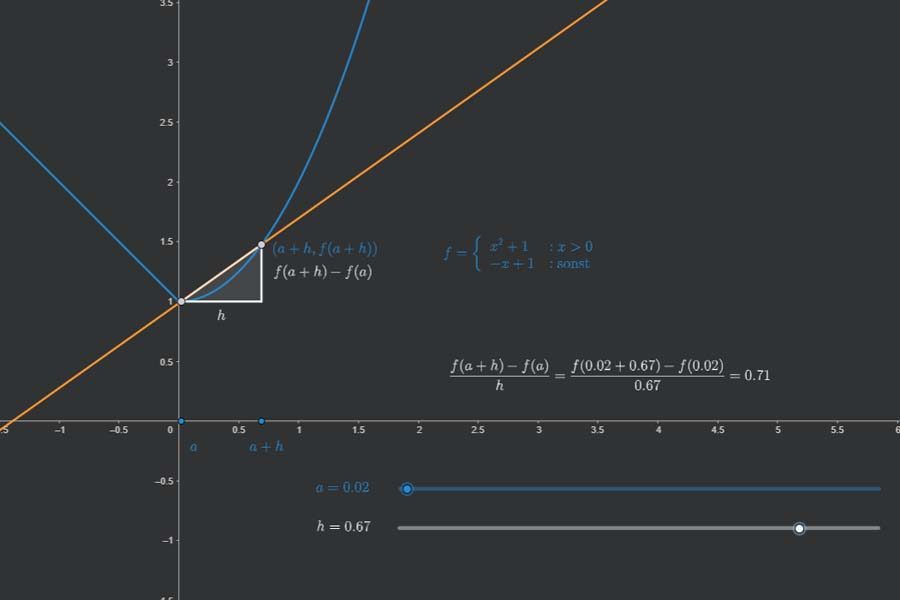
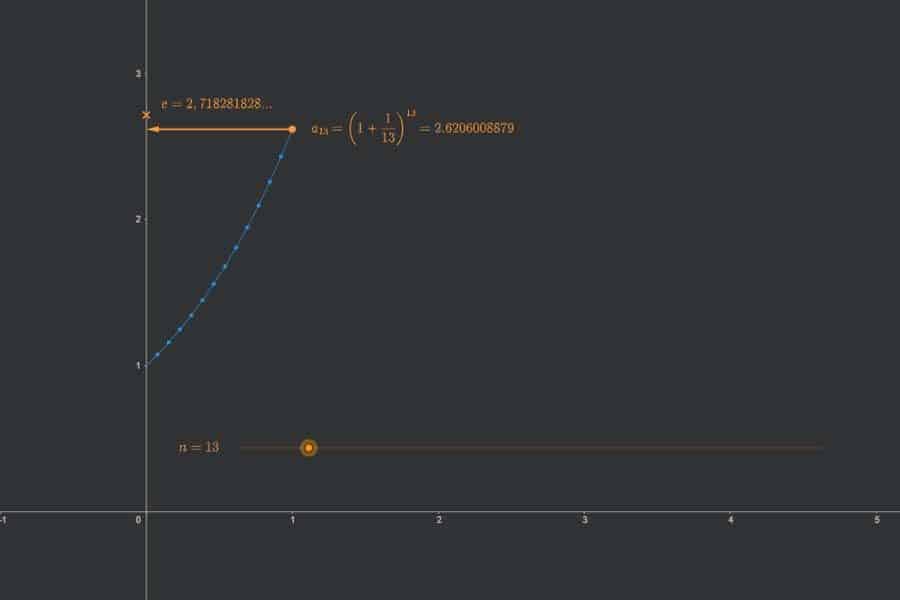
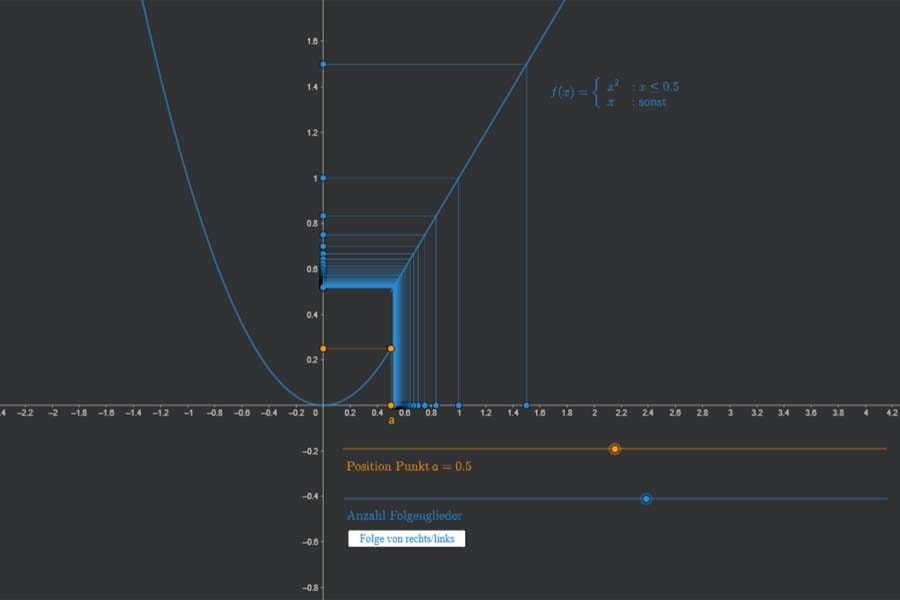
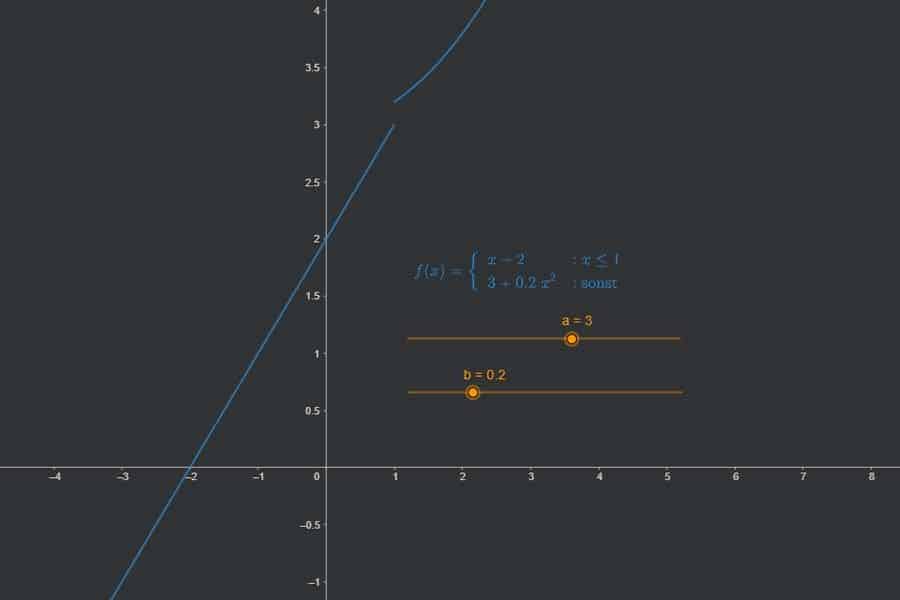











Interaktiv: Ableitung der Umkehrfunktion