Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Eine der beeindruckendsten Arten, sich die Wirkungsweise der Fourieranalyse vor Augen zu führen, ist die Rekonstruktion einer beliebigen geschlossenen Kurve durch so genannte Epizykeln, d. h. durch Kreise, die auf Kreisen sitzen, die auf Kreisen sitzen, die auf…


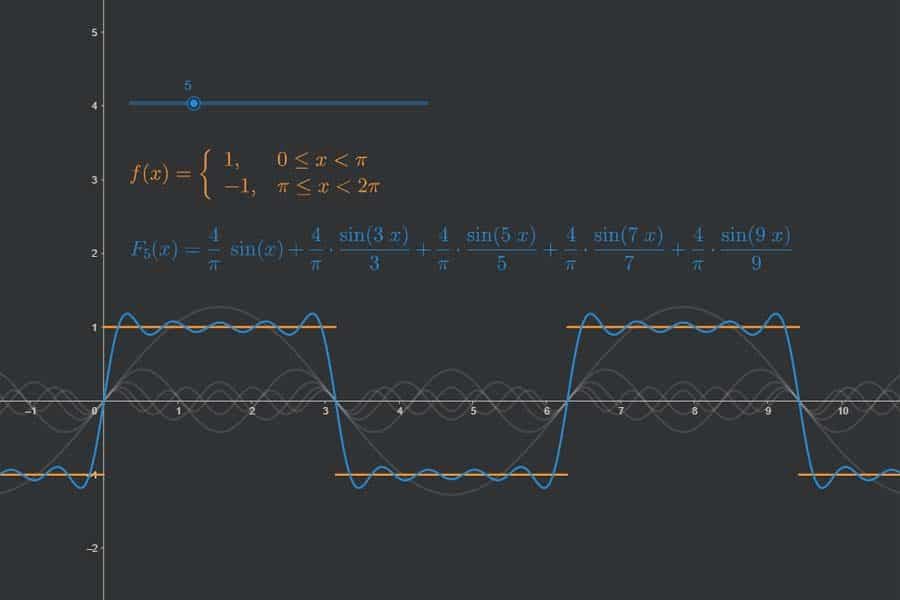
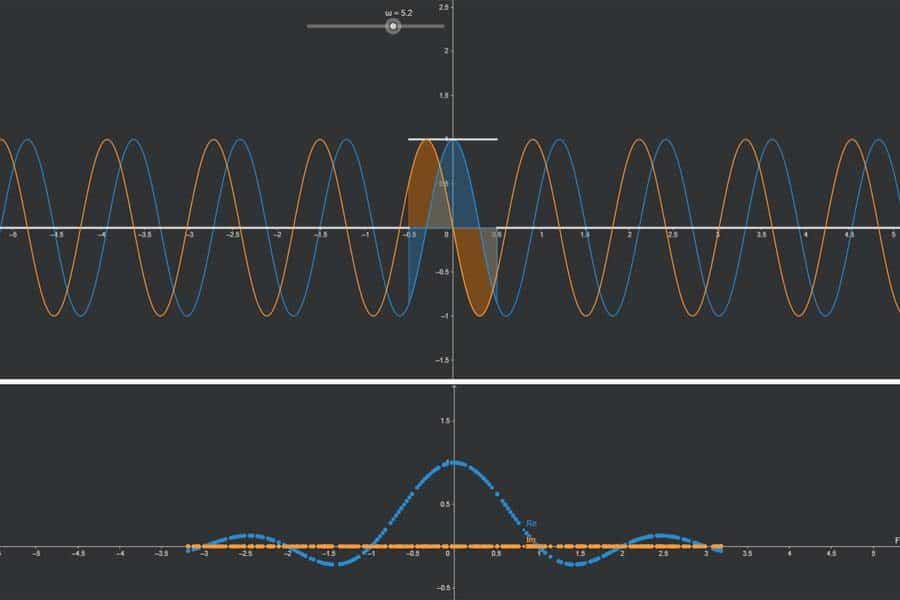
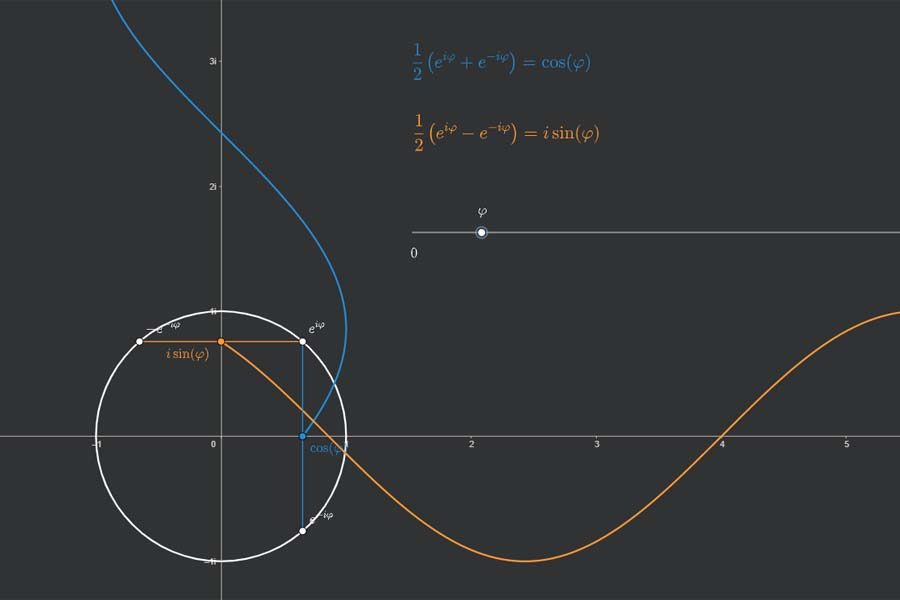
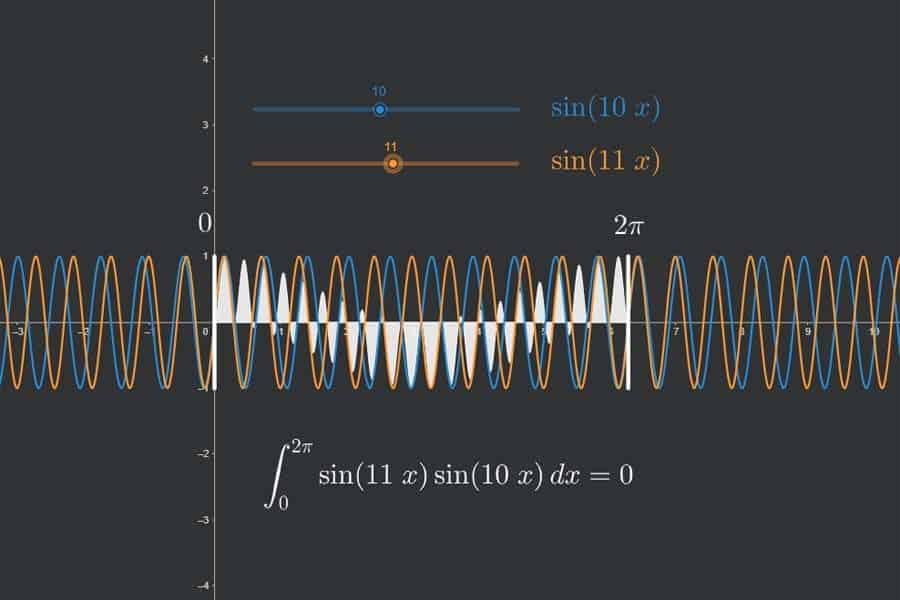
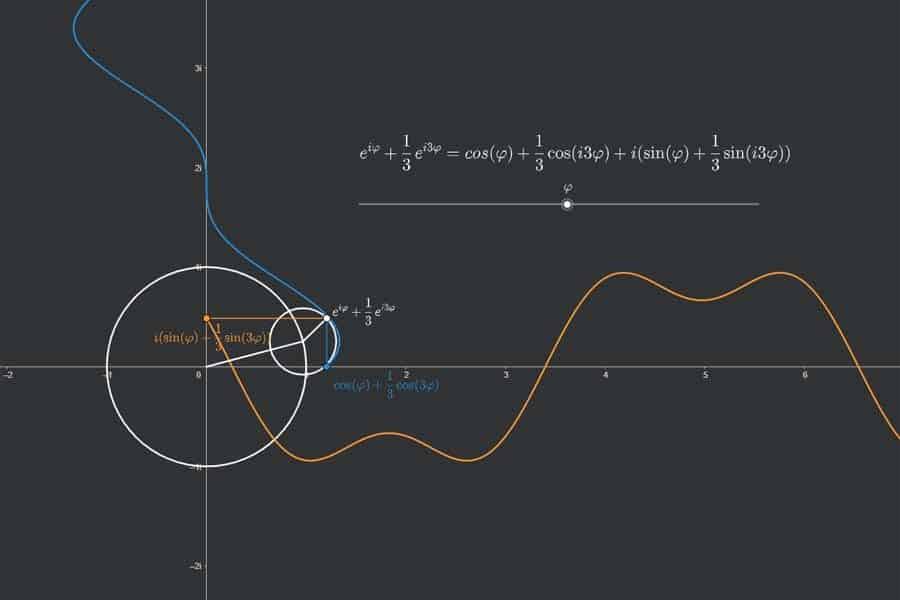
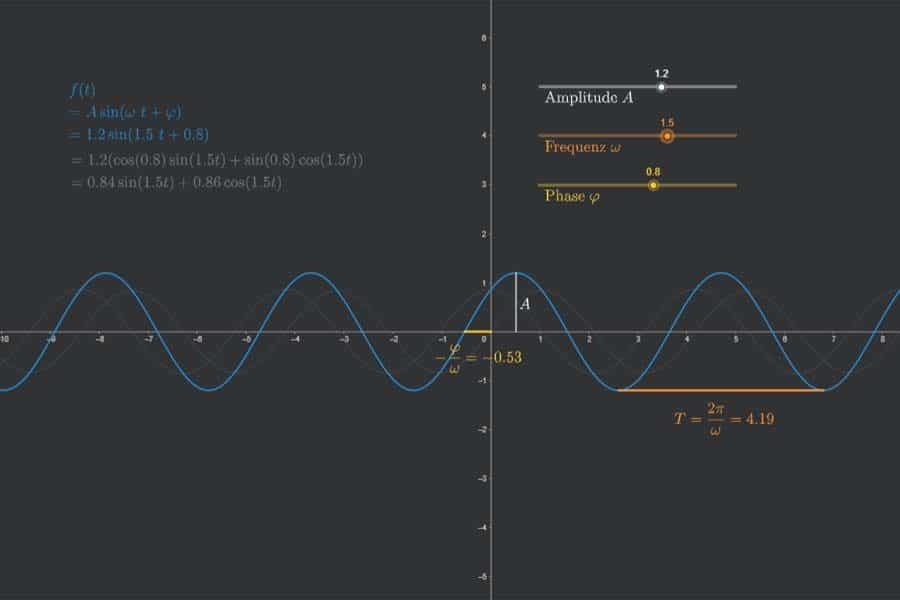
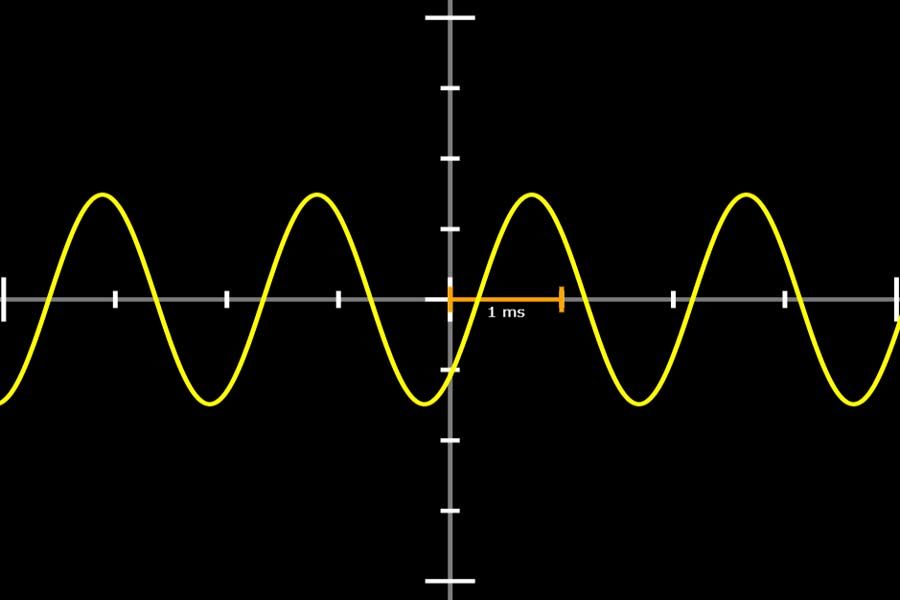
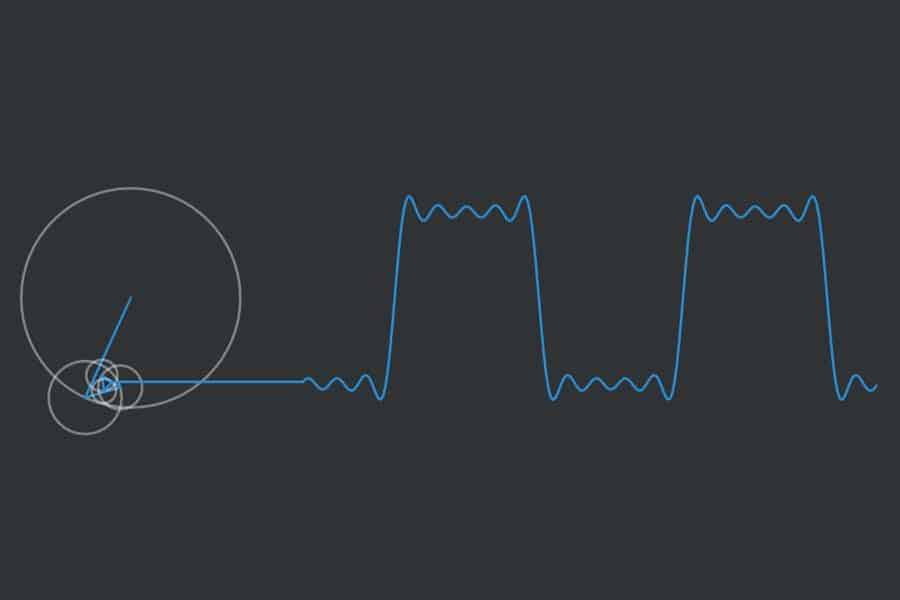












Interaktiv: Fourier-Synthese