Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Bastelstunde! Wir schrauben aus einzelnen Sinus- und Kosinusschwingungen eine zusammengesetzte periodische Funktion zusammen. Wie? Indem wir die „Lautstärken“ (Amplituden) der einzelnen Teilschwingungen einstellen. Die Kombination dieser Lautstärken definieren das Aussehen der zusammengesetzten Funktion.


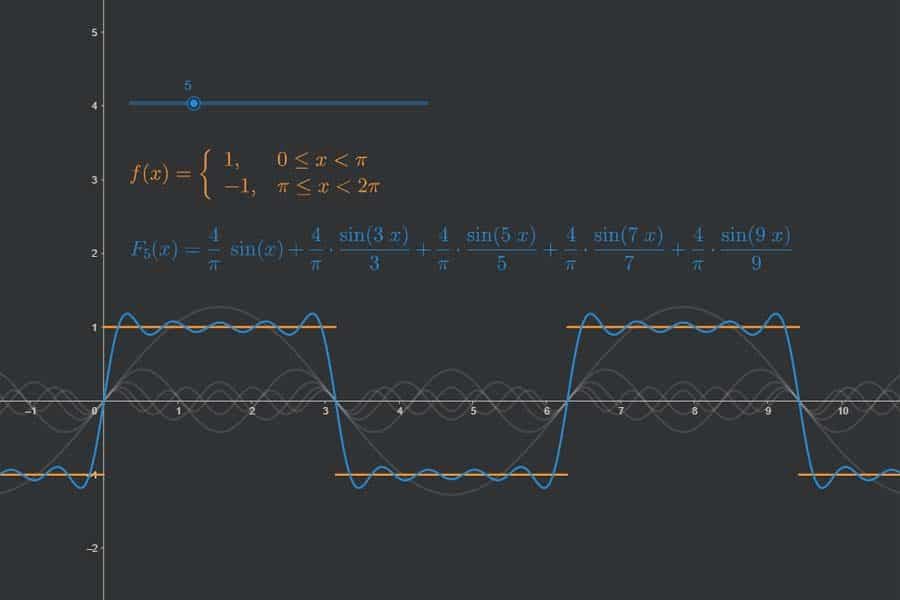
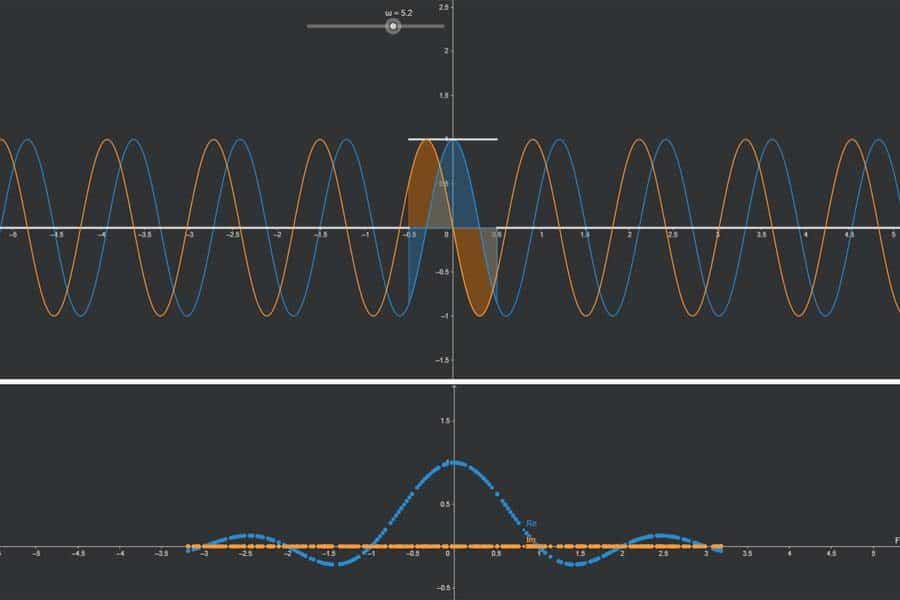
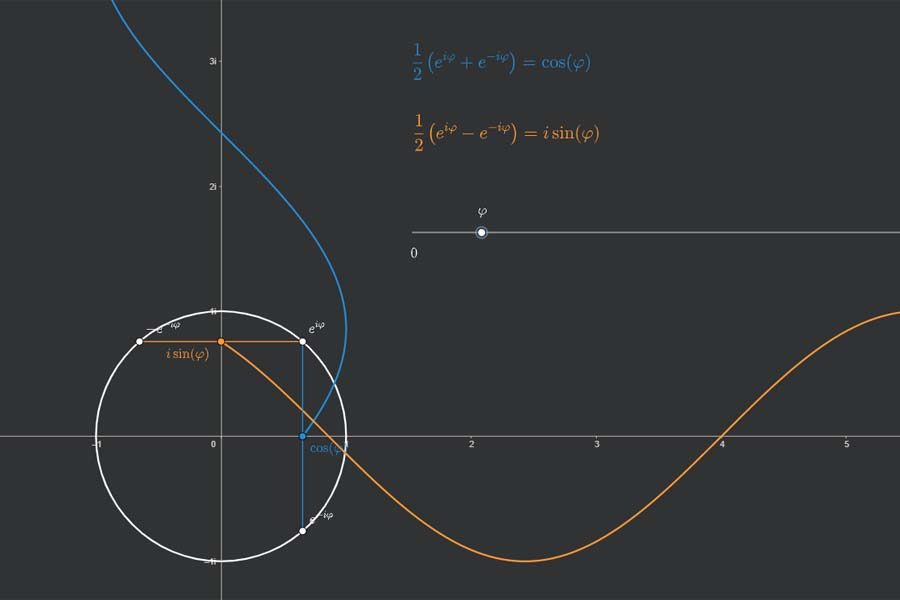
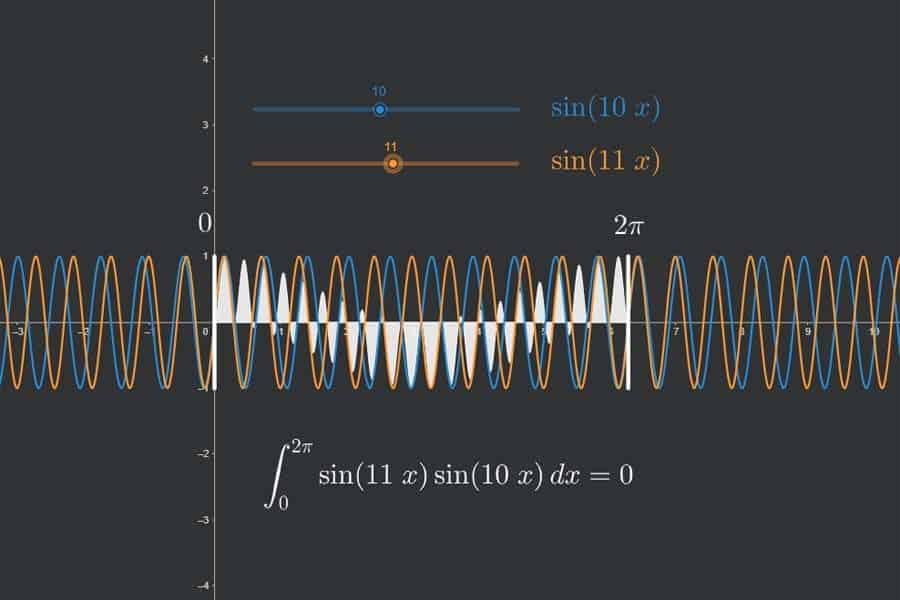
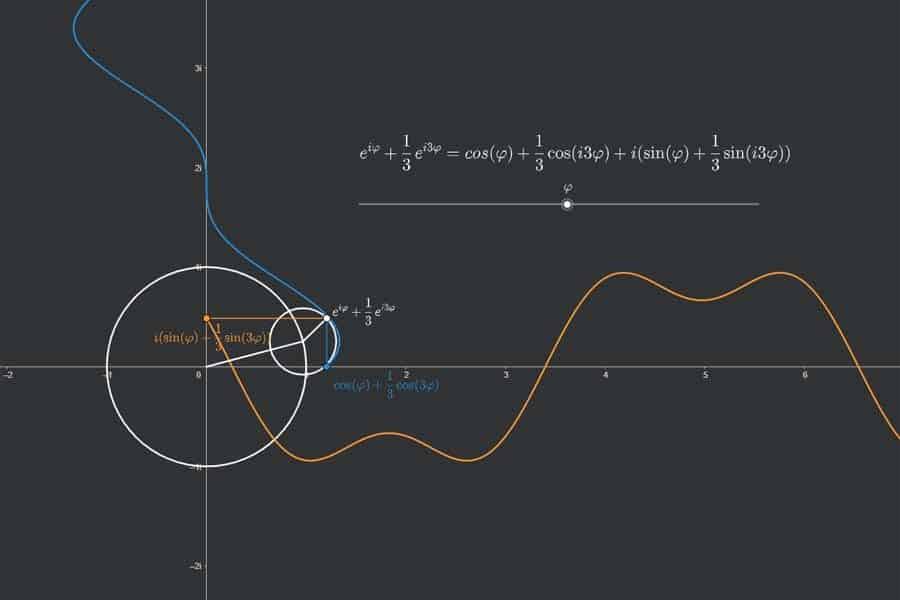
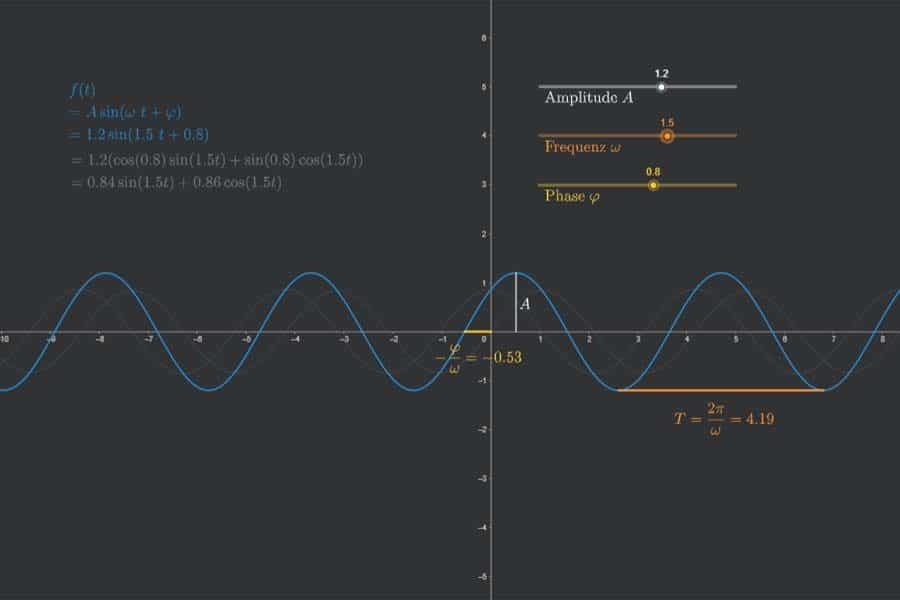
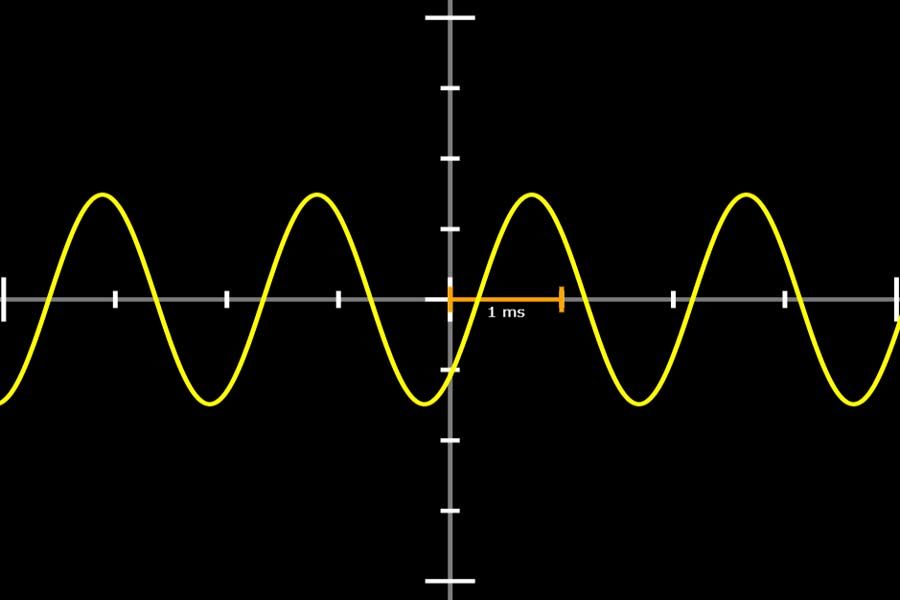
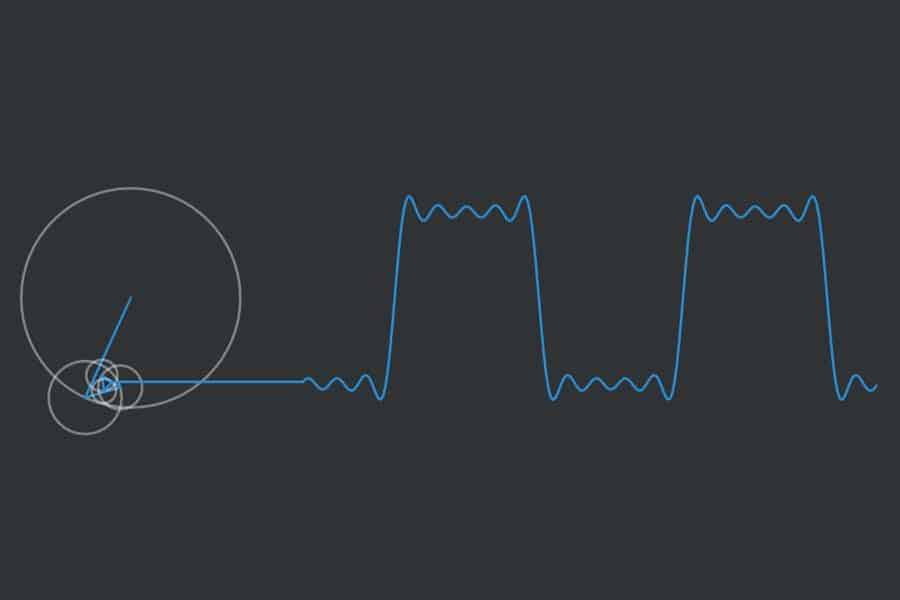












Interaktiv: Fourier-Synthese