Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Bei Sinus und Kosinus kann man an rechtwinklige Dreiecke denken (Gegenkathete durch Hypotenuse und so) oder man kann an die wohlbekannten Schwingungen denken. Was aber hat das eine mit dem anderen zu tun? Die Antwort ist einfach, liegt aber etwas verborgen im Einheitskreis.


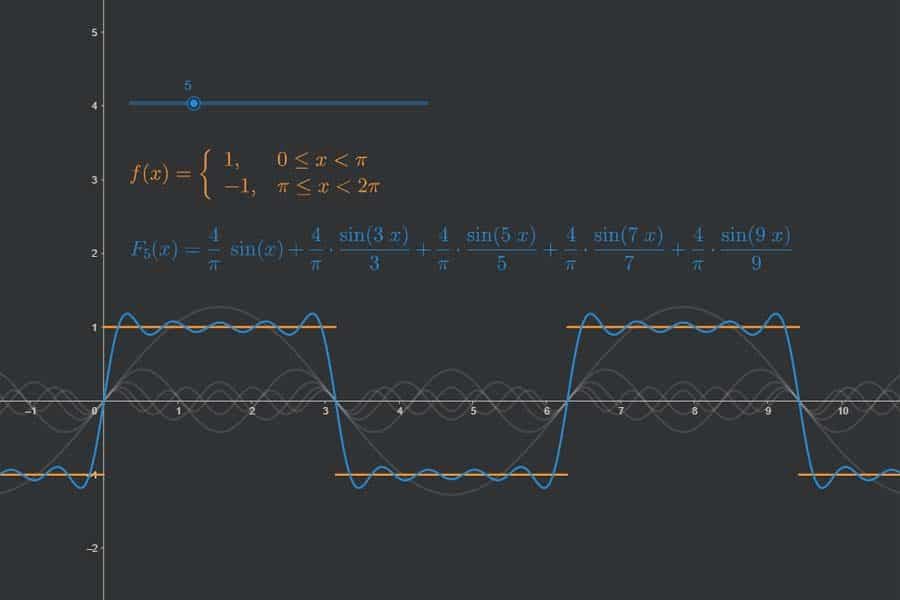
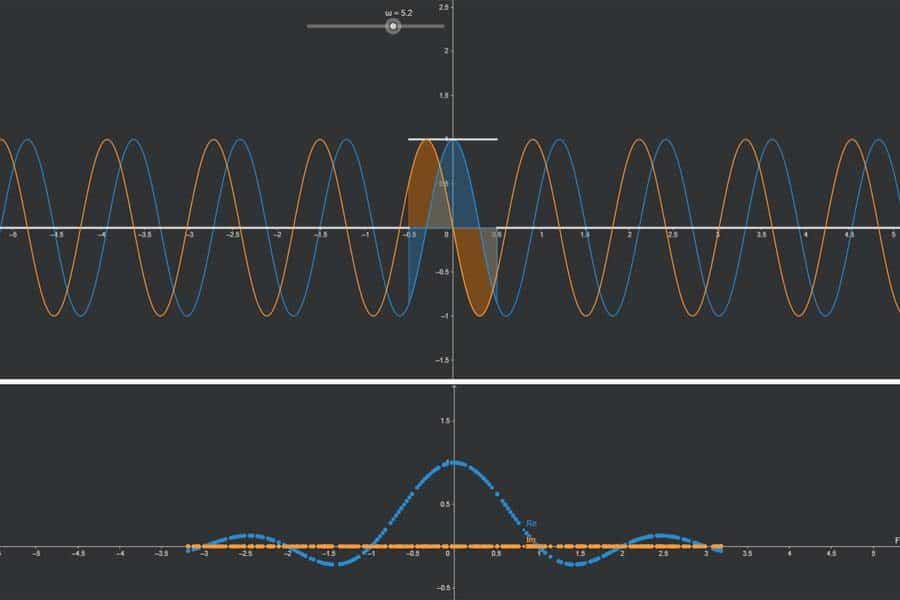
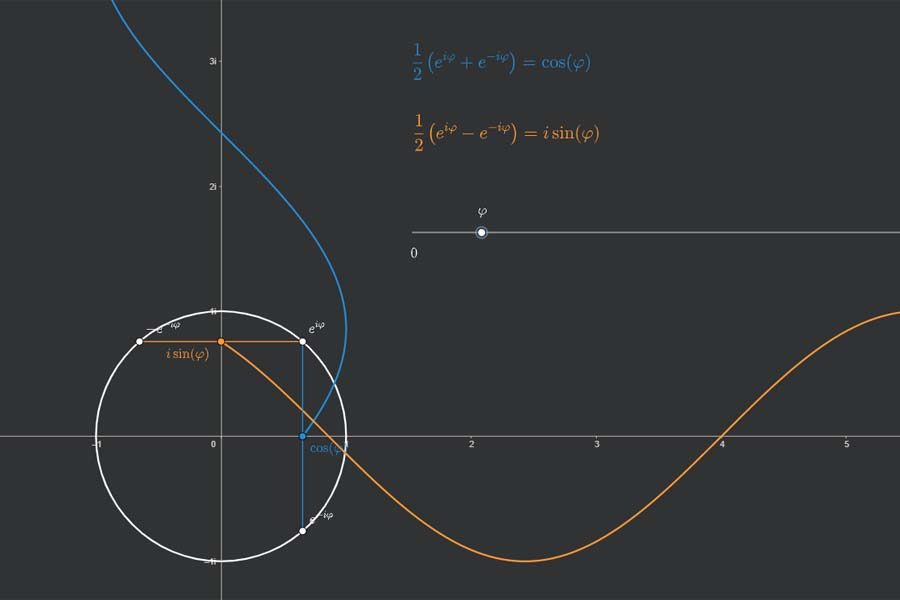
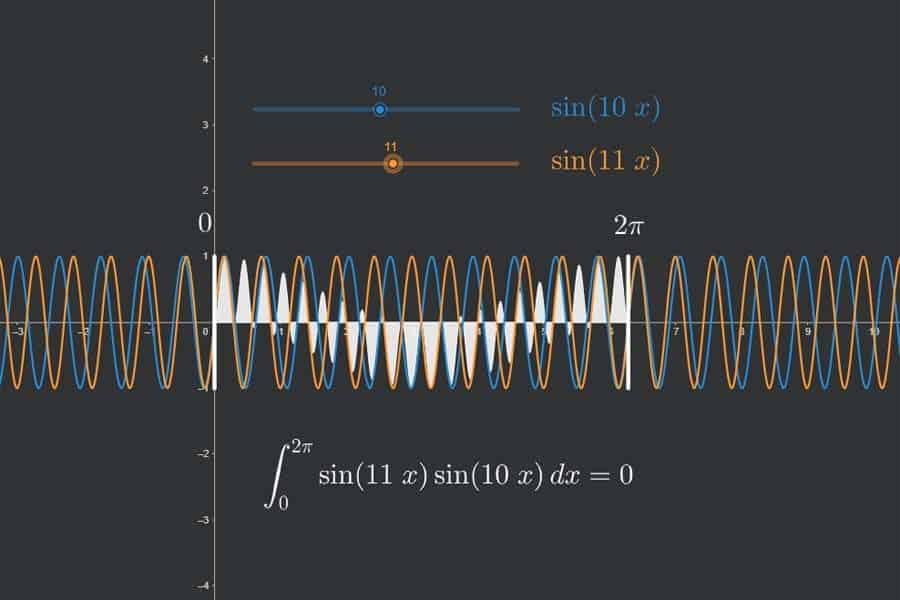
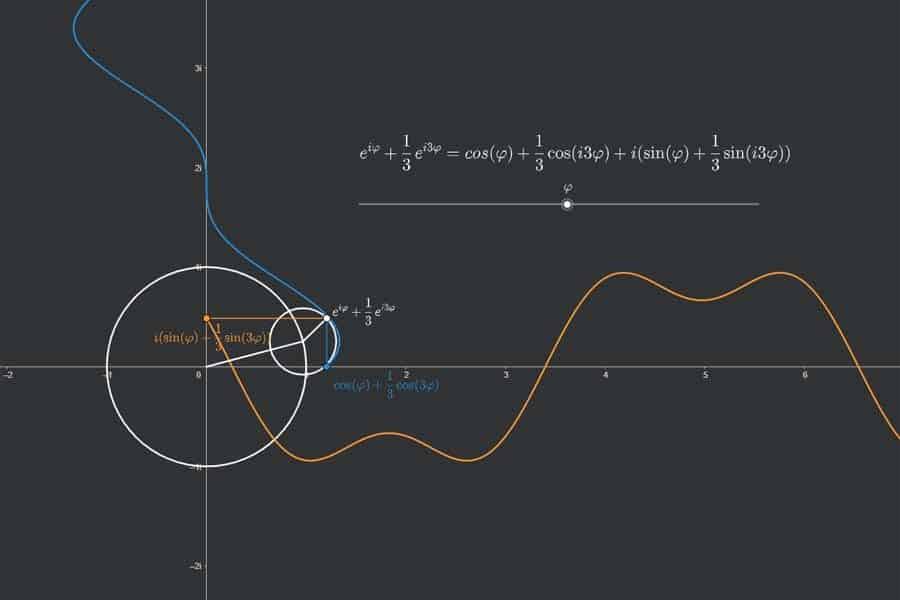
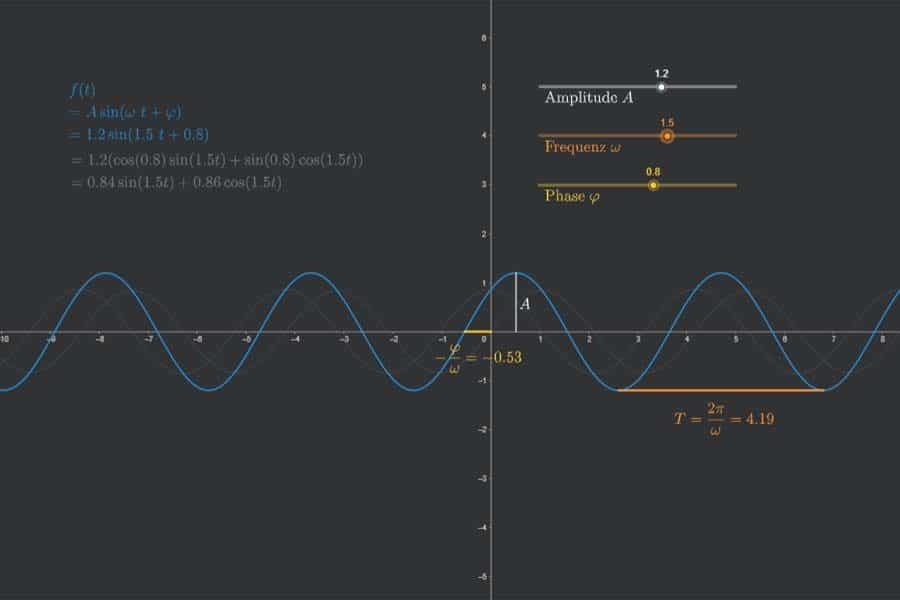
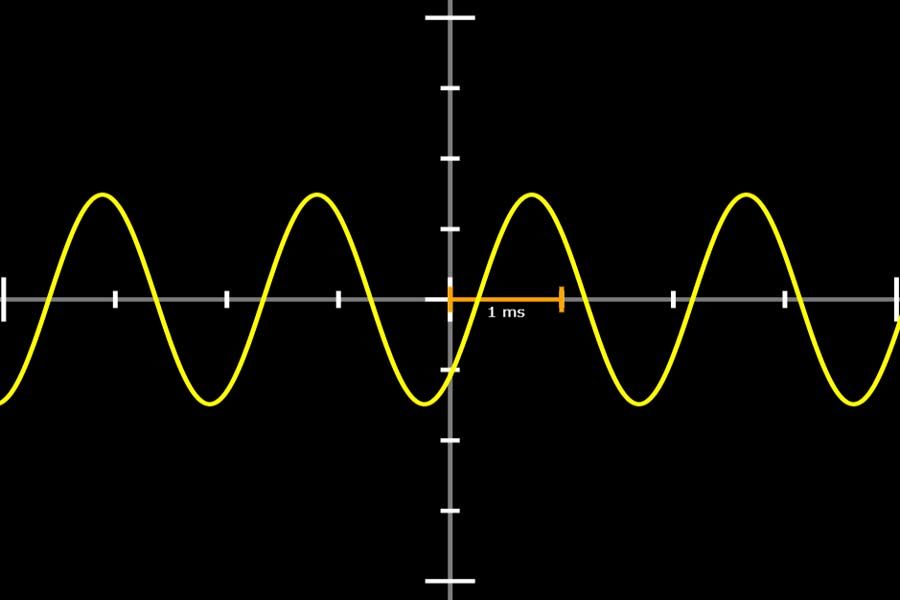
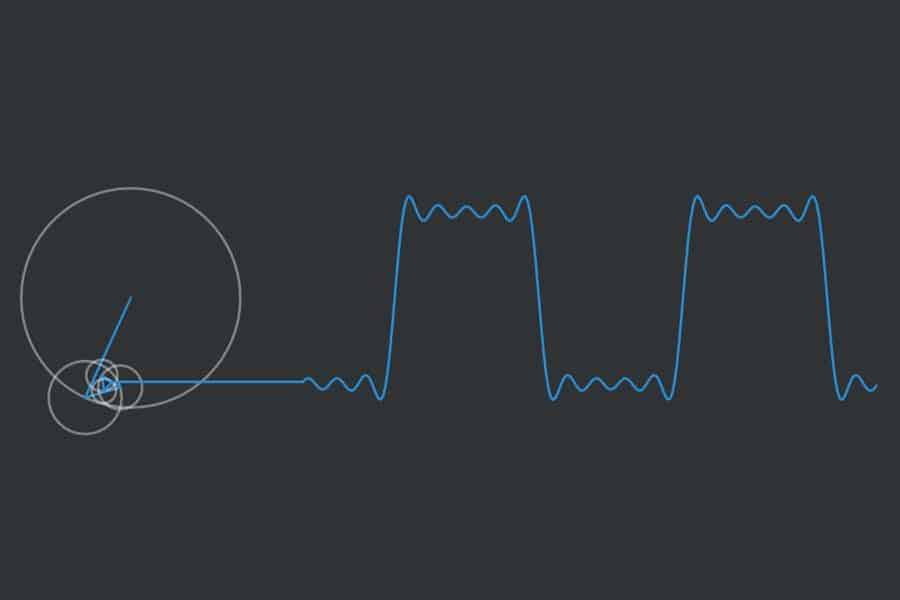












Interaktiv: Fourier-Synthese