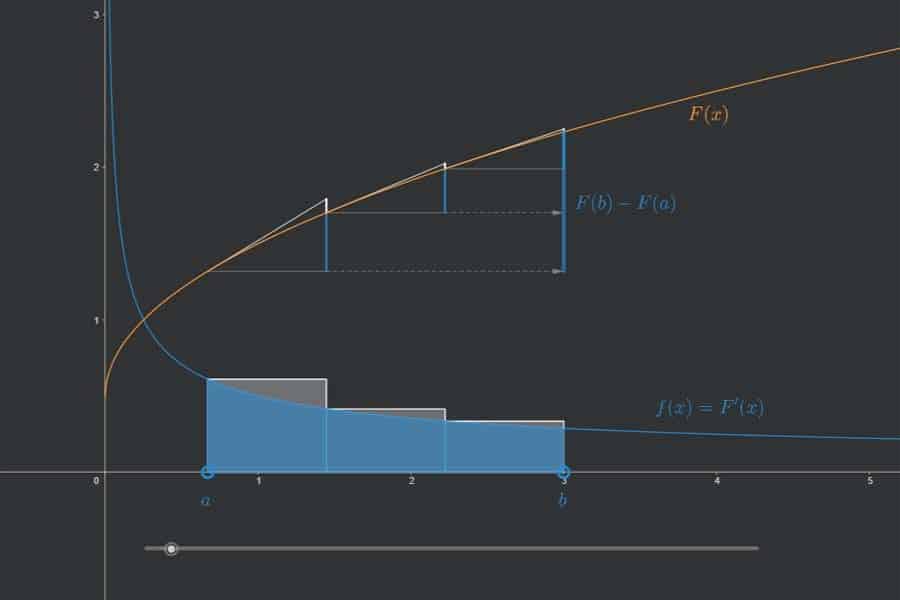
Die App veranschaulicht den Hauptsatz der Differential- und Integralrechnung. Dieser besagt, dass das bestimmte Integral einer Funktion f zwischen a und b berechnet werden kann als die Differenz F(b)-F(a), wobei F eine (beliebige) Stammfunktion von f ist.
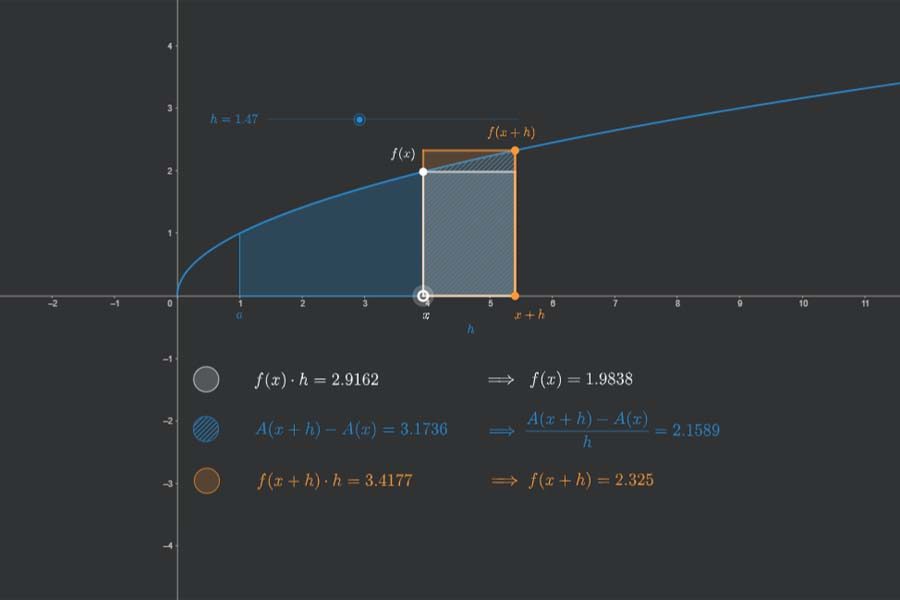
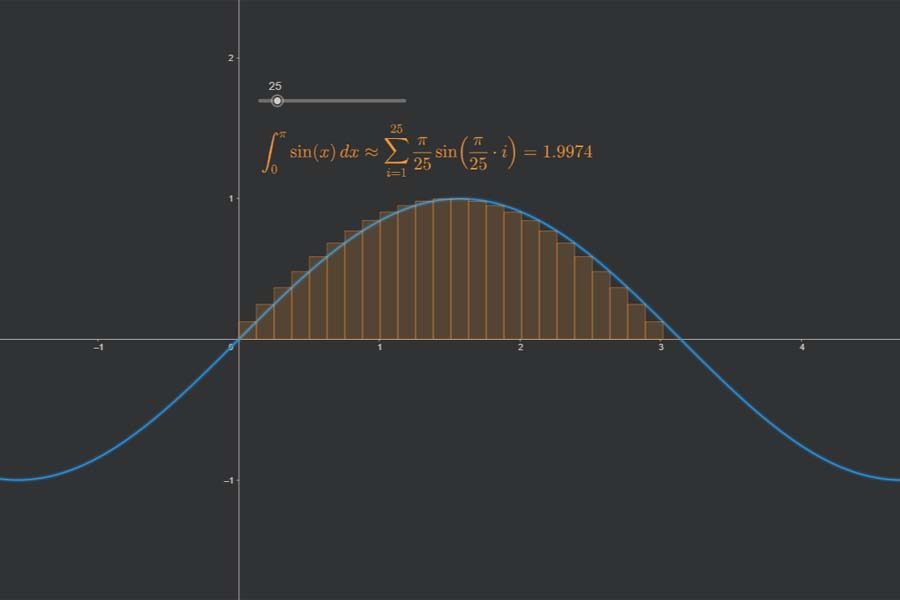
Näherungsweise lässt sich das Integral von f (blaue Funktion) als die Summe der Flächeninhalte von „Säulen“ (Rechtecken) ermitteln, die die betroffene Fläche näherungsweise abdecken, siehe Riemann-Integral. Dabei ergeben sich Fehler (weiße Teilflächen der Säulen) gegenüber der korrekten Fläche (blaue Teilflächen). Mit dem Schieberegler lässt sich die Anzahl der Säulen verändern. Beobachte, wie bei höheren Anzahlen die weißen „Fehlerflächen“ kleiner werden – nicht nur jede einzelne, sondern auch alle in Summe betrachtet (was nicht unmittelbar klar ist).
Die Säulen sind so gewählt, dass ihre Höhe genau dem Funktionswert von f an ihrer jeweiligen linken Seite entspricht. Die orangefarbene Funktion F ist eine Stammfunktion von f. Daher haben die Tangenten an F an diesen linken Säulenseiten (gelbe Linien) eine Steigung, die dem dortigen Wert von f entspricht (nichts anderes bedeutet Stammfunktion).
Multipliziert man die Höhe einer Säule mit der Säulenbreite (nennen wir sie h), so erhalten wir die Fläche der Säule. Spannt man mit der Tangente an F an der linken Säulenseite ein Steigungsdreieck der Breite h auf, dann weist die vertikale Seite dieses Dreiecks (in der App blau-weiß dargestellt; den weißen Teil sieht man nur, wenn man mit dem Schieberegler eine kleine Säulenzahl einstellt, z. B. 3) eine Länge auf, die genau dem Flächeninhalt der Säule entspricht (Das ist der Witz an der Sache: Eine Länge entspricht jetzt einem Flächeninhalt!).
„Stapelt“ man alle diese vertikalen Dreiecksseiten (jeweils bestehend aus blauem und weißem Teilstück) aufeinander, dann erhält man also die Summe aller Säulenflächen (welche ja beinahe, aber eben nur beinahe dem Integral von f zwischen a und b entspricht). Tatsächlich repräsentieren die weißen Teilstücke der vertikalen Dreiecksseiten jeweils genau den Fehler, um den sich die jeweilige Säule bei der Ermittlung der Fläche zwischen f und x-Achse „verschätzt“. Schön wäre es, wenn die weißen „Fehler-Teilstücke“ gar nicht vorhanden wären, denn dann bestünden die vertikalen Dreiecksseiten nur aus dem jeweiligen blauen Teilstück, die – aufeinandergestapelt bzw. aufsummiert – genau F(b)-F(a).
Das ist aber kein Problem, denn wir haben noch einen Trumpf in der Hand: Lässt man nun nämlich die Anzahl der Säulen gegen unendlich gehen (der Schieberegler erlaubt das „näherungsweise“ ;-)), dann werden die weißen „Fehler-Teilstücke“ schnell kleiner (und zwar „deutlich“ schneller als die Säulenbreiten), und alles löst sich in Wohlgefallen auf: Die Summe der „unendlich dünnen Säulen“ entspricht einerseits genau dem Flächeninhalt zwischen f und der x-Achse (also dem Integral von f zwischen a und b); andererseits ist diese Summe exakt gleich groß wie die Summe der vertikalen Dreiecksseiten, bei denen man nun den weißen Anteil vernachlässigen darf (das ist die eigentliche Krux!), so dass diese Summe exakt dem Wert F(b)-F(a) entspricht.


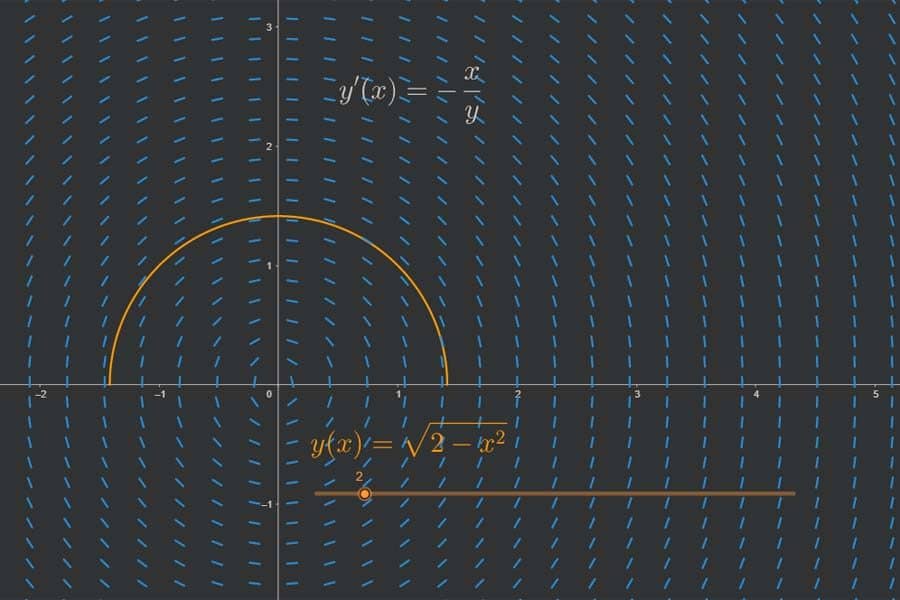
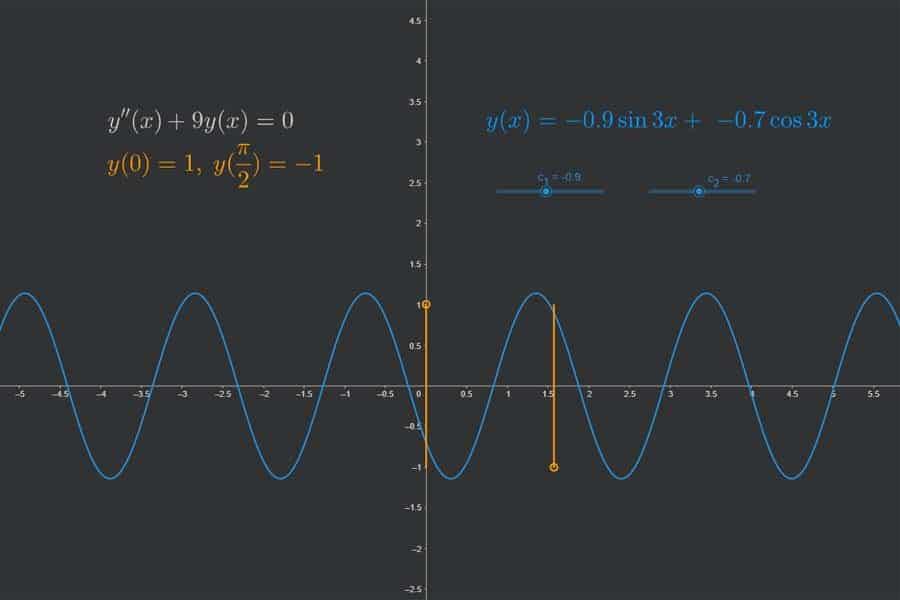

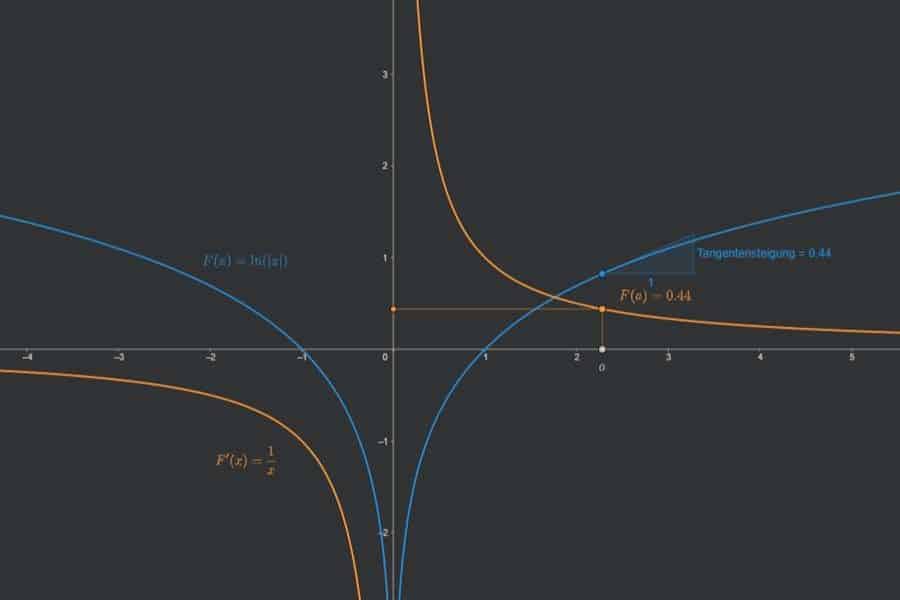











Interaktiv: Richtungsfeld und Trajektorien einer Differentialgleichung