Manche Differentialgleichungen lassen sich besonders griffig mit Steigungsfeldern illustrieren.
Differentialgleichungen kann man als Vorgabe verstehen, auf welche Weise eine Funktion (die „Lösung“) sich verändern soll (in Raum oder Zeit). Veränderung lässt sich auch als Steigung verstehen. Besonders griffig lässt sich das für Differentialgleichungen erster Ordnung veranschaulichen, wenn sie als Steigungsfeld zeichnet, welchem eine Lösungskurve folgen muss. In der Regel gibt es bei einem Steigungsfeld mehrere Möglichkeiten, Lösungskurven (Trajektorien, zu deutsch „Wurfkurven“) hineinzulegen.


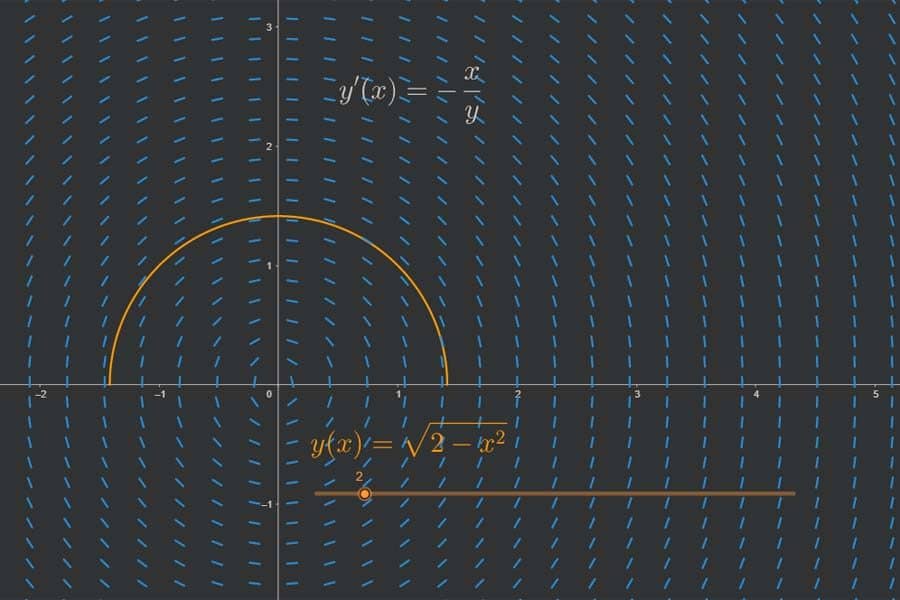
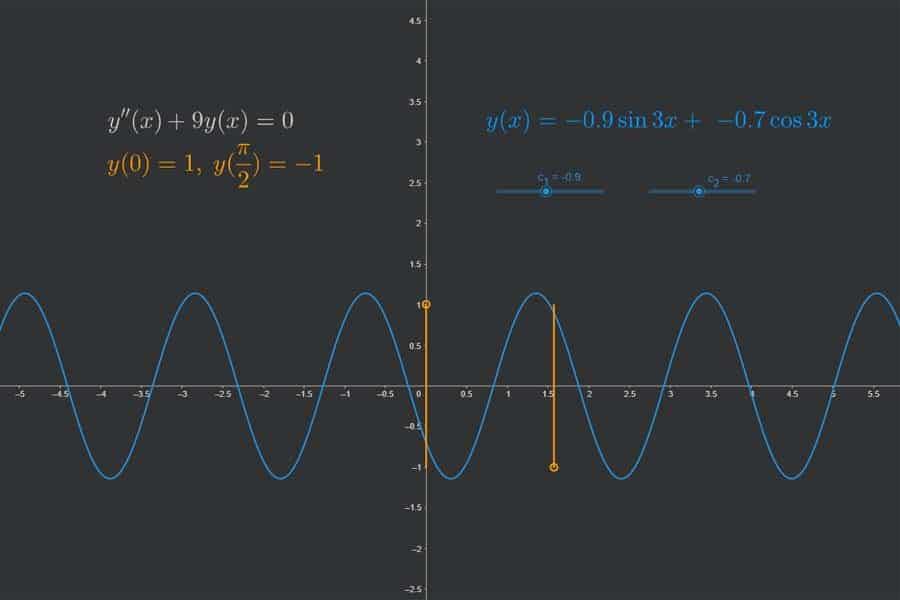












Interaktiv: Richtungsfeld und Trajektorien einer Differentialgleichung