Interaktiv: Zweidimensionale Fläche und partielle Ableitungen

Funktionen von zwei Variablen. Schön anschaulich darstellbar als Flächen im dreidimensionalen Raum. Sofern diese Flächen „knickfrei“ sind, sind sie auch differenzierbar, d. h. man kann an jedem Punkt einmal die Steigung in x-Richtung und einmal die Steigung in y-Richtung messen. Tut man dies an jedem Punkt, dann bilden diese beiden Steigungswerte in Abhängigkeit vom Punkt wieder jeweils eine Funktion von zwei Variablen. Und so weiter.

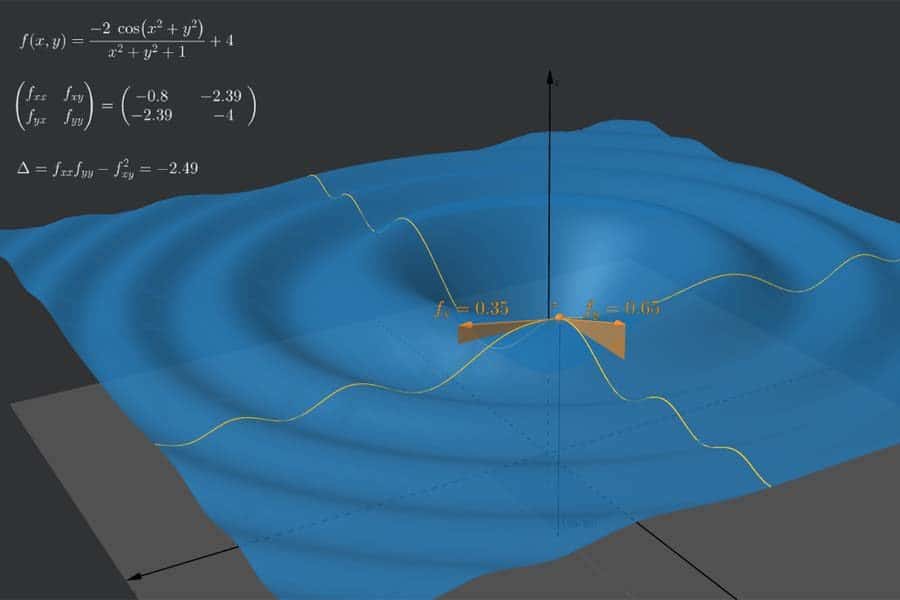
Die weiße Fläche stellt den zweidimensionalen Funktionsgraph der in der weißen Formel angegebenen Funktion f von zwei Variablen dar. Der schwarze Punkt P in der Fläche kann mit der Maus bewegt werden. Beobachte dabei, wie sich der blaue und der orangefarbene Vektor ändert. Diese stellen die ersten beiden partiellen Ableitungen von f (blau: nach x, orange: nach y) dar. Sie stellen die Steigungen der beiden Schnittkurven in x- bzw. y-Richtung (blau bzw. orange) dar. Wenn beide Steigungen sind, dann ist P ein Extrempunkt oder ein Sattelpunkt. Beide partielle Ableitungen kann man selbst auch wieder als Funktionen von zwei Variablen auffassen (blauer und orangefarbener Funktionsgraph).